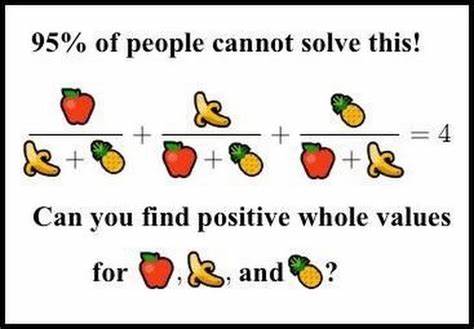Nachdem die Internetkultur über Jahre hinweg von scheinbar simplen Rechenaufgaben mit Emojis oder Früchten dominiert wurde, steht eine besondere Klasse von mathematischen Problemen hervor, die nicht nur zur Unterhaltung dient, sondern tiefgehende mathematische Konzepte offenbaren. Insbesondere ein virales „Emoji-Mathematik“-Problem mit komplexen Frucht-Bildgleichungen erwies sich als mehr als nur ein spaßiger Zeitvertreib. Es braucht die Anwendung hochentwickelter mathematischer Werkzeuge, nämlich die Theorie elliptischer Kurven, um dieses Meme wirklich zu durchdringen und eine vollständige Lösung zu finden. Diese Herangehensweise illustriert eindrucksvoll, wie reine Mathematik, die oft als abstrakt wahrgenommen wird, auf moderne, alltägliche Phänomene angewandt werden kann und eröffnet einen faszinierenden Blick in die Tiefe des Zahlentheorie-Universums. Die elliptischen Kurven sind dabei nicht einfach nur eine technische Methode, sondern ein universelles Werkzeug, das es erlaubt, komplexe Gleichungen zu entschlüsseln, indem man auf der Menge ihrer rationalen Punkte operiert.
Die Herausforderung, die hinter dem viralen Emoji-Mathematik-Problem versteckt ist, hängt mit der Suche nach ganzzahligen oder rationalen Lösungen polynomieller Gleichungen zusammen, deren Komplexität exponentiell ansteigt, sobald kleine Änderungen an der Aufgabenstellung vorgenommen werden. Wo klassische algebraische Methoden versagen, treten elliptische Kurven als mächtiges Instrument hervor. Das Fundament dieser Methode liegt darin, dass man das Problem von einer Suche nach diskreten Ganzzahllösungen auf eine Suche nach rationalen Punkten auf einer sogenannten elliptischen Kurve überführt. An dieser Stelle beginnt die Magie: Eine elliptische Kurve ist eine spezielle Cubic-Kurve mit einem dehnbaren algebraischen Aufbau, der sowohl eine geometrische Interpretation als auch eine Gruppenstruktur besitzt. Diese Struktur ermöglicht eine systematische Erzeugung neuer rationaler Punkte durch sogenannte „Punktaddition“.
Konkret bedeutet dies, dass man zwei bekannte rationalen Punkte auf der Kurve verbinden und durch eine wohl definierte Formel einen neuen rationalen Punkt erhalten kann. Dieses Verfahren zeigt sich äußerst elegant, denn selbst wenn der Ausgangspunkt trivial ist, lässt sich durch wiederholtes Anwenden der Punktaddition eine unendliche Anzahl an Lösungen erschließen – zumindest theoretisch. In der Praxis sind die Rechenwege komplex und die Größenordnung der Lösungen kann schnell ins Gigantische wachsen. Für das virale Emoji-Problem – das auf den ersten Blick wie ein simples Rechenpuzzle wirkt – ergibt sich nach einer Transformation der ursprünglichen Darstellung eine elliptische Kurve, die nicht nur in der Lage ist, Lösungen jenseits einfacher Raten oder Ausprobierens zu bieten, sondern auch tieferliegende mathematische Prinzipien sichtbar macht. Die Identifikation geeigneter rationaler Punkte auf der Kurve ist dabei vor allem eine Frage strategischen Vorgehens.
Für bekannte einfache Punkte, beispielsweise jene, die durch die ursprüngliche Problemstellung nahegelegt werden, ist das Ergebnis nur von begrenztem Wert, da sich daraus keine „ausbruchsartigen“ neuen Lösungen ergeben – diese Punkte gehören zur sogenannten Torsionsgruppe, bei der durch wiederholte Addition keine neuen Punkte entstehen. Doch durch eine Ausweitung auf Punkte unendlicher Ordnung, oft über computerunterstützte Berechnungen, etwa mit Programmen wie Mathematica, ist es möglich, „entferntere“ Lösungen zu erzeugen, die das eigentliche Ziel – positive, ganzzahlige Lösungen – näherbringen. Die Anwendung dieser Vorgehensweise ist technisch herausfordernd, da jede neue Lösung häufig mit immer größerer Zahlendarstellung erkauft wird. Die Verarbeitung und Handhabung solcher Zahlenmengen sprengt mühelos die Grenzen ausschließlich manueller Berechnung und erfordert daher unbedingt den Einsatz leistungsfähiger Algorithmen und Computerrechenleistung. Diese Symbiose von moderner Computermathematik und klassischer Zahlentheorie stellt das Herzstück der Herangehensweise an das Emoji-Problem dar.
Gleichzeitig fungiert sie als exemplarisches Beispiel dafür, wie die Mathematik komplexe, scheinbar spielerische Herausforderungen meistern kann. Darüber hinaus illustriert das zugrundeliegende Prinzip der elliptischen Kurven auch prominentere Anwendungen, etwa in der Kryptographie. Die mathematische Struktur, die hier zur Lösung eines Meme-Problems eingesetzt wird, bildet dieselbe Basis, auf der hochsichere Verschlüsselungstechniken fußen. Dies unterstreicht den Wert der mathematischen Forschung jenseits rein akademischer Interessen mit realweltlichen Auswirkungen. Zusammenfassend lässt sich sagen, dass elliptische Kurven essentiell dazu befähigen, schwierige Gleichungen mit ganzzahligen oder rationalen Lösungen nicht nur zu durchdenken, sondern systematisch zu lösen – eine Rolle, die in der Vergangenheit der Mathematik nur wenigen Werkzeugen zuteilwurde.
Das mathematische Meme, das als Ausgangspunkt diente, erweist sich so als Tor zu einem faszinierenden Universum und bietet einen Einblick in die tiefen Verbindungen zwischen Algebra, Geometrie, Zahlentheorie und moderner Technologie. Wer sich mit elliptischen Kurven auseinandersetzt, entdeckt nicht nur elegante mathematische Konstruktionen, sondern auch eine Brücke zwischen theoretischem Wissen und praktischen Anwendungen, was den Reiz und die Bedeutung dieser Methode im 21. Jahrhundert eindrucksvoll unterstreicht. Dieses Wissen kann nicht nur mathematische Rätselfreunde begeistern, sondern auch eine Inspiration darstellen, um komplexe Probleme mit Ausdauer, Kreativität und modernster Technologie anzugehen.