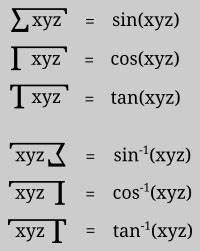Die Mathematik lebt von präziser Kommunikation, besonders in den Bereichen der Physik und höheren Mathematik, wo komplexe Konzepte oft nur durch elegante und genaue Notationen verständlich werden. Die Feynman-Trig-Notation ist ein fortschrittliches Werkzeug, das dabei hilft, mathematische Ausdrücke klarer darzustellen, insbesondere im Zusammenhang mit trigonometrischen Funktionen. Doch der wahre Fortschritt zeigt sich darin, wie Nutzer eigene Zeichen anpassen und erstellen können, um den spezifischen Anforderungen ihrer Arbeit oder ihres Forschungsgebiets gerecht zu werden. Das Verständnis und die Nutzung der Feynman-Trig-Notation eröffnen neue Möglichkeiten für Wissenschaftler, Studenten und alle mathematisch Interessierten, die über herkömmliche Symbole hinausgehen möchten. Die klassische trigonometrische Notation besteht meist aus Standardfunktionen wie Sinus, Kosinus oder Tangens, die in vielen Lehrbüchern und wissenschaftlichen Arbeiten verwendet werden.
Doch in bestimmten Kontexten, besonders in der theoretischen Physik oder bei komplexen mathematischen Beweisen, sind zusätzliche Symbole notwendig, um Zusammenhänge präziser zu beschreiben. Richard Feynman, ein renomierter Physiker, dessen Name eng mit innovativen Didaktikmethoden und der Quantenmechanik verknüpft ist, legte mit der Feynman-Trig-Notation einen Grundstein für kreative Darstellungsformen. Diese erlaubt es, trigonometrische Funktionen nicht nur auszudrücken, sondern durch Variationen in den Zeichen und deren Kombinationen eine tiefere Bedeutung zu transportieren. So kann eine speziell angefertigte Notation nicht nur mathematische Beziehungen darstellen, sondern auch gedankliche Prozesse und intuitives Verständnis visualisieren. Das Erstellen und Anpassen eigener Zeichen wird durch moderne Typografie-Technologien und Tools für mathematische Formate erheblich erleichtert.
TeX und LaTeX beispielsweise bieten umfassende Möglichkeiten, neue Symbole und Operatoren zu definieren, die auf bestehenden mathematischen Notationen aufbauen oder komplett neue Konzepte einführen. Die Integration in LaTeX-Dokumente stellt sicher, dass die Zeichen korrekt, skalierbar und konsistent dargestellt werden, was gerade bei wissenschaftlichen Veröffentlichungen von größter Bedeutung ist. Individuelle Zeichen können dabei verschiedene Funktionen erfüllen. Sie dienen nicht nur der Vereinfachung komplizierter Ausdrücke, sondern auch der besseren Nachvollziehbarkeit komplexer Argumente. Visuelle Hervorhebungen oder spezielle Kombinationen machen es möglich, bestimmte Aspekte hervorzuheben oder zwischen verschiedenen Subtypen mathematischer Konstrukte zu unterscheiden.
So trägt die Feynman-Trig-Notation mit der Fähigkeit zur Anpassung zur Effizienz der Kommunikation bei und erlaubt eine präzise Differenzierung, die mit Standardnotationen schwer umzusetzen ist. Ein weiterer wichtiger Aspekt ist die didaktische Komponente. Gerade in Bildungs- und Forschungskontexten fördert die Möglichkeit, eigene Zeichen zu entwickeln, das Verständnis und die Kreativität der Lernenden. Statt sich auf vorgegebene Symbole zu beschränken, können Lehrende und Studierende mit individuellen Notationen experimentieren, die ihre eigenen Denkprozesse besser reflektieren. Das erleichtert das Erfassen komplexer Sachverhalte und erlaubt einen direkteren Zugang zu abstrakten Inhalten.
Die Feynman-Trig-Notation kombiniert also das Beste aus zwei Welten: mathematische Strenge und kreative Freiheit. Durch das Erschaffen von eigenen Symbolen entsteht eine neue Form der Ausdrucksmöglichkeit, die nicht nur funktional, sondern auch ästhetisch ansprechend ist. Dies kann in Forschungsarbeiten dazu beitragen, die Aufmerksamkeit des Lesers zu halten und wichtige Punkte hervorzuheben, während gleichzeitig die mathematische Exaktheit gewahrt bleibt. Die praktische Umsetzung des Erstellens eigener Zeichen erfordert allerdings ein gewisses Maß an technischem Verständnis, insbesondere im Umgang mit Software wie LaTeX oder speziellen Grafikprogrammen. Wer sich mit den Grundlagen dieser Tools vertraut macht, kann jedoch schnell und effizient eigene Erweiterungen anfertigen.
Online-Ressourcen, Foren und Communities bieten zudem umfassende Unterstützung und Beispiele, wie Feynman-Trig-Notation individuell gestaltet werden kann. Im heutigen Zeitalter der digitalen Wissensvermittlung ist die Anpassungsfähigkeit der Notation fast ebenso wichtig wie deren Inhalt. Wissenschaftliche Dokumente werden nicht nur auf gedrucktem Papier gelesen, sondern auch auf Bildschirmen, Tablets und mobilen Geräten. Daher müssen eigene Zeichen sowohl in unterschiedlichen Auflösungen als auch in verschiedenen Softwareumgebungen einwandfrei funktionieren. Die Feynman-Trig-Notation und ihre individualisierbaren Charaktere erfüllen diese Anforderungen durch standardisierte Kodierungen und einfache Einbindung.
Fazit ist, dass die Feynman-Trig-Notation weit mehr ist als nur eine weitere mathematische Formel. Sie ist ein Werkzeug für Innovation und persönliches Ausdrucksvermögen in einer Sprache, die sonst oft als starr und unflexibel wahrgenommen wird. Das Erstellen eigener Zeichen ermöglicht nicht nur die genaue Beschreibung komplexer trigonometrischer Sachverhalte, sondern fördert auch das kreative Denken und die Entwicklung neuer mathematischer Ideen. Wer sich mit dieser Notation auseinandersetzt und eigene Zeichen kreiert, erweitert nicht nur seine mathematischen Fähigkeiten, sondern trägt auch zur Weiterentwicklung der wissenschaftlichen Kommunikation bei.