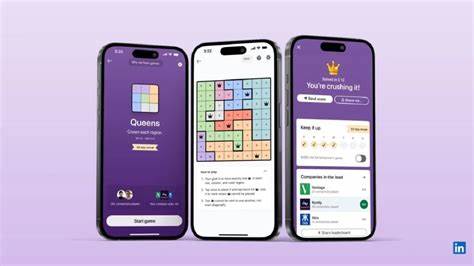
LinkedIn, bekannt als berufliches Netzwerk, hat eine wenig beachtete, aber faszinierende ganze Reihe von Spielen in seiner Plattform integriert, die vielen Nutzern bislang verborgen geblieben sind. Eines dieser Spiele, Queens, basiert auf einem klassischen mathematisch-logischen Problem, dem N-Queens-Problem. Dieses beschäftigt sich mit der Herausforderung, auf einem Schachbrett der Größe N×N N Damen so zu platzieren, dass keine zwei Damen sich in einer Reihe, Spalte oder Diagonale bedrohen. Zwar ein altbekanntes Thema, doch hat die Kombination mit moderner Software und Logik einen ganz neuen Anwendungsfall geschaffen: Die Jagd nach dem Weltrekord auf LinkedIn in Queens durch die Methode der Reduktion auf SAT-Probleme. Dieses exponentiell komplexe Problem und seine Lösungsansätze wollen wir im Folgenden näher beleuchten.
Die Verbindung klassischer Informatik und moderner Spiele eröffnet spannende Einblicke in Praxis und Theorie gleichermaßen. Das SAT-Problem, auch bekannt als das Problem der erfüllbaren booleschen Formeln, gehört zu den zentralen Fragestellungen der theoretischen Informatik und ist NP-vollständig. Konkret geht es darum, für eine gegebene logische Formel herauszufinden, ob es eine Belegung der enthaltenen Variablen gibt, die die gesamte Formel wahr macht. Die Schwierigkeit liegt dabei in der potenziell astronomischen Anzahl möglicher Kombinationen. Mit einer Anzahl von Variablen n wächst die mögliche Anzahl an Belegungen exponentiell mit 2 hoch n.
Praktische SAT-Solver nutzen jedoch mittlerweile ausgeklügelte Algorithmen und Heuristiken, um dieses laut theoretischer Literatur unüberschaubare Suchfeld massiv einzuschränken und so oft sehr schnell eine Lösung zu finden. Um das N-Queens-Problem auf ein SAT-Problem zu übertragen, muss man zunächst sämtliche möglichen Platze für eine Dame auf dem Spielfeld als jeweils eine Variable betrachten. Für ein 9×9-Brett etwa ergibt das 81 Variablen, bei denen jede angibt, ob eine Dame an einer bestimmten Position steht oder nicht. Die Kernfrage des SAT-Solvers lautet: Gibt es eine Belegung dieser Variablen, die alle Spielregeln berücksichtigt? Dazu müssen mehrere Einschränkungen und Bedingungen in die logische Formel eingebaut werden. Erstens muss sichergestellt sein, dass in jeder Reihe und jeder Spalte genau eine Dame steht.
Zweitens dürfen sich keine zwei Damen auf einer diagonalen Linie befinden, welche sie bedrohen könnte. Die Schwierigkeit bei der Formulierung liegt darin, die Bedingungen korrekt und zugleich möglichst effizient als boolesche Formeln zu schreiben. Ein Missverständnis hierbei ist oft, nur „at most one“ (höchstens eine) Dame pro Reihe oder Spalte zu fordern. Dies ist jedoch nicht ausreichend, denn die Spielregeln verlangen, dass es „exactly one“ (genau eine) Dame sein muss. Dieses Problem kann gelöst werden, indem man die Formel als Kombination von „at most one“ und „at least one“ Bedingungen zusammenfasst.
Die „at least one“-Bedingung lässt sich dabei sehr einfach durch Verknüpfung der Variablen in einer Reihe oder Spalte mit einer logischen „oder“-Verknüpfung umsetzen. Für „at most one“ benötigt man komplexere Formelbausteine, die garantieren, dass keine zwei verschiedenen Positionen gleichzeitig mit einer Dame besetzt werden können. Hierbei kommen logische Implikationen und Negationen zum Einsatz, etwa dass wenn an Position A eine Dame steht, an Position B keine sein darf, und dies für alle Kombinationen von Positionen innerhalb derselben Reihe, Spalte oder Diagonale. Durch geschickte Programmierung und Optimierung dieses Verfahrens wird oft die Anzahl der nötigen Klauseln reduziert, was eine entscheidende Rolle bei der Performance der SAT-Solver spielt. Das ursprüngliche N-Queens-Problem wurde auf diese Weise erfolgreich in vielen Anwendungen gelöst.
LinkedIns Queens erweitert das Problem jedoch durch veränderte Regeln und zusätzliche Constraints. So fehlt in dieser Variante die klassische Diagonalbedingung. Stattdessen kommen neue Auflagen hinzu: Es muss eine Dame pro Reihe, Spalte und sogar pro Farbe (Farbklassifikation der Felder) vorhanden sein, und zudem darf keine Dame neben einer anderen stehen, also keine benachbarte Position in jeglicher Richtung (horizontal, vertikal oder diagonal) von einer Dame besetzt sein. Daraus ergeben sich neue Herausforderungen für die SAT-Formulierung, da die Beschränkungen noch komplexer und teilweise gegensätzlicher sind. Die Farbebene gibt einen völlig neuen Parameter vor, der in der klassischen N-Queens-Version keine Rolle spielt.
Außerdem verändert sich die Bedeutung der Diagonalen, denn nur unmittelbare Nachbarschaften diagonal benachbarter unterschiedlicher Farben müssen berücksichtigt werden, die aufeinander keinen Einfluss haben dürfen. Für die praktische Umsetzung wurde eine Methode entwickelt, die zunächst alle Felder mit Farbinformationen abspeichert und anschließend für jedes Feld die diagonal benachbarten Felder mit abweichender Farbe erkennt. Diese Nachbarn werden dann als sogenannte "Edges" abgebildet, welche spezielle Einschränkungen in der SAT-Formel erhalten. Um zu verhindern, dass zwei Damen auf benachbarten Feldern stehen, muss für jede dieser "Edges" gelten, dass höchstens eine der beiden Positionen mit einer Dame belegt sein darf. Diese Problematik förderte neue Überlegungen zur optimalen Formulierung von atMostOne-Constraints.
Die Möglichkeit, diese Einschränkungen doppelt zu generieren – ausgehend von beiden Nachbarfeldern – wurde zwar erkannt, aber aufgrund der hohen Effizienz moderner SAT-Solver zunächst als vernachlässigbar eingestuft. Dennoch bietet dieses Thema Raum für weitere Optimierungen und Performance-Verbesserungen bei der Modellierung. Das Ergebnis dieses komplexen Ansatzes ist eine umfassende boolesche Formel, die alle Regeln des LinkedIn Queens-Spiels abbildet – Reihen- und Spaltenzwang, Farbzwang sowie die strikte Nachbarschaftsregel. Eine derartige Formulierung macht es SAT-Solvern möglich, in vergleichsweise kurzer Zeit gültige Lösungen zu finden, die vorher nur mit manueller Eingabe, Heuristiken oder Backtracking bewältigt werden konnten. Die praktische Umsetzung erfolgte mit einem Solver namens CVC5, einem modernen SMT- und SAT-Solver, der sich durch seine Geschwindigkeit und Effizienz auszeichnet.
In Kombination mit einer speziell entwickelte Firefox-Erweiterung und einem Python-Backend konnten die Puzzle-Daten aus LinkedIn extrahiert, in geeignete SAT-Formate überführt, gelöst und anschließend die Lösung über die Erweiterung auf dem Spielbrett umgesetzt werden. So war es möglich, automatisiert und zuverlässig valide Spielzüge zu berechnen und auszuführen. Die Umsetzung führte nicht nur zum persönlichen Erfolg des Entwicklers, der damit den Weltrekord im LinkedIn Queens-Spiel erlangte, sondern demonstriert eindrucksvoll die Leistungsfähigkeit moderner Logik und Mathematik in der Praxis. Dabei trifft eine zeitlose Fragestellung der Informatik auf ein modernes digitales Spiel, das auf den ersten Blick trivial scheint, es aber durch kluge Abstraktion und Technik in ein Machine-Learning- und KI-ähnliches Setting überführt. Hinzu kommt der Mehrwert, der sich aus der Verbindung einer theoretischen Problematik und einer interaktiven, realitätsnahen Anwendung ergibt.
Die Arbeit zeigt eindringlich, wie klassische Probleme von der akademischen Umklammerung gelöst auf die Straße gebracht werden können. Dies eröffnet neue Wege für Entwickler, Informatiker und KI-Interessierte, sich mit Kompetenzen im Bereich der Reduktion komplexer Probleme auf SAT und andere logische Formate auseinanderzusetzen. In einer Zeit, in der Games und spielerische Umgebungen immer wichtiger werden, bieten solche Projekte spannende Möglichkeiten für die Forschung, für Bildung sowie für die Unterhaltung. Wer sich auf LinkedIn künftig an Queens versucht, kann sich bewusst machen, dass hinter jeder Herausforderung eine faszinierende Welt aus mathematischer Logik und algorithmischer Raffinesse steht – und dass moderne Software in der Lage ist, scheinbar harte Grenzen mit Intelligenz und Berechnung zu überwinden. Abschließend belegt der Erfolg bei LinkedIns Queens die herausragende Rolle von SAT-Solvern in unterschiedlichsten Anwendungsgebieten weit über ihre eigentliche Definition hinaus.
Ob Spiele, Planung, Verifikation oder Optimierung – die Fähigkeit, komplexe Entscheidungsprobleme algorithmisch zu modellieren und lösen, ist ein zentrales Werkzeug der digitalen Zukunft. Die Kombination mit offenen Plattformen, praktischen Programmierschnittstellen und Browser-Erweiterungen zeigt zudem den aktuellen Stand der Technik im Bezug auf Integration und User Experience. Durch das bewusste Zusammenspiel von Hardcore-Logik, moderner Programmierung und spielerischem Wettbewerb wurde mit LinkedIns Queens ein bemerkenswertes Beispiel geschaffen, das jedes Technikinteresse weckt und zeigt, wie tief anspruchsvoll scheinende Aufgaben in der Praxis gemeistert werden können. Dieses Projekt ermutigt dazu, sich selbst mit logischen Herausforderungen auseinanderzusetzen, neue Fähigkeiten zu erlernen und die Potenziale der Informatik für unterhaltsame und gleichzeitig anspruchsvolle Anwendungen zu nutzen.