Terence Tao: Der Weg zur Formalisierung eines Beweises in Lean4 mit Claude und o4

Terence Tao, einer der bedeutendsten Mathematiker unserer Zeit, hat sich stets durch außergewöhnliche Begabung und das Streben nach Präzision ausgezeichnet. In jüngster Zeit richtet sich sein Interesse verstärkt auf die Formalisierung mathematischer Beweise mithilfe moderner Technologien. Besonders die Kombination von Lean4, Claude und dem Tool o4 eröffnet neue Wege, um komplexe mathematische Argumente präzise und überprüfbar auf digitale Plattformen zu übertragen. Dieser Prozess ist nicht nur technisch hoch anspruchsvoll, sondern birgt auch das Potenzial, die Arbeitsweise in der Mathematik grundlegend zu verändern. Die Formalisierung von mathematischen Beweisen bedeutet, dass diese in eine Sprache übersetzt werden, die von Computern überprüft werden kann.

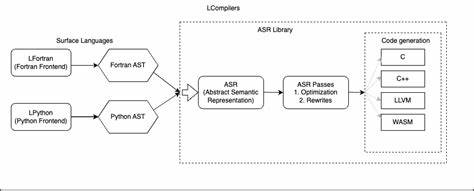
Lean4, eine Weiterentwicklung des Lean-Proof-Assistenten, ist hierbei eine der leistungsfähigsten Umgebungen. Es erlaubt Mathematikern, ihre Argumente mit strenger logischer Struktur zu formulieren und gleichzeitig von der maschinellen Überprüfung zu profitieren. Dies minimiert Fehlerquellen, die in menschlichen Beweisen gelegentlich auftreten können, und erhöht die Zuverlässigkeit der mathematischen Erkenntnisse. Die Rolle von Claude, einem fortschrittlichen KI-System, ist in diesem Zusammenhang besonders bemerkenswert. Claude unterstützt dabei, sprachliche und konzeptionelle Barrieren bei der Übersetzung von informellen mathematischen Darstellungen in die formale Sprache von Lean4 zu überwinden.

Diese assistierende Technologie fungiert als Brücke zwischen der menschlichen Intuition und der maschinellen Präzision. Im Zusammenspiel mit o4, einem spezialisierten Werkzeug zur Organisation und Prüfung von Beweisen in Lean, entstehen damit leistungsstarke Werkzeuge zur Beweisformaliserung. o4 optimiert die Arbeitsabläufe, indem es etwa Abhängigkeiten zwischen Elementen visualisiert und den Beweisprozess strukturierter gestaltet. Das Ergebnis ist ein Ökosystem, das Mathematikern zugutekommt, weil es sowohl die Effizienz steigert als auch die Genauigkeit verbessert. Terence Tao demonstriert in einem aufschlussreichen Video, wie er mit Hilfe dieser Technologien einen bestimmten Beweis formalisiert.

Dabei wird nachvollziehbar, wie sich ein abstraktes mathematisches Konzept durch schrittweise Formalisierung in Lean4 niederschreiben lässt. Das Video illustriert den praktischen Ablauf und macht die Vorteile neuer Tools wie Claude und o4 für die mathematische Praxis greifbar. Diese Entwicklung ist Teil einer breiteren Bewegung, die akademische Mathematik zunehmend mit digitaler Technologie verknüpft. Die digitale Formalisierung von Beweisen kann langfristig zu einer revolutionären Veränderung führen, bei der mathematische Theorien nicht nur von Menschen geschrieben und überprüft werden, sondern zusätzlich von Algorithmen analysiert und validiert werden. Das bietet immense Chancen für Fortschritte in Theorie, Lehre und Anwendung.

Die Vorteile einer präzisen maschinellen Verifikation sind weitreichend. Sie reichen von der schnelleren Publikation sicherer Ergebnisse bis hin zu neuen Formen der Zusammenarbeit zwischen Mathematikern weltweit. Dank solcher Tools können komplexe Beweise modular aufgebaut und mit anderen Forschern geteilt werden, was die Transparenz und Nachvollziehbarkeit erhöht. Darüber hinaus birgt die Integration von KI-unterstützten Systemen wie Claude die Möglichkeit, Routinearbeiten beim Schreiben und Überprüfen von Beweisen zu automatisieren. Das verschafft Mathematikern mehr Zeit für kreative und innovative Aufgaben.

Gleichzeitig fordert es aber auch ein Umdenken in der Ausbildung zukünftiger Fachkräfte, die zunehmend mit solchen Technologien vertraut sein müssen. Die Arbeit von Terence Tao mit Lean4, Claude und o4 steht exemplarisch für diese neue Ära der Mathematik. Es zeigt, wie exzellente theoretische Kenntnisse gepaart mit der Offenheit für technologische Innovationen zu bemerkenswerten Ergebnissen führen können. Diese Kombination fördert eine präzisere, kollaborative und effizientere Wissensproduktion. Neben den offensichtlichen Vorteilen gibt es jedoch auch Herausforderungen.