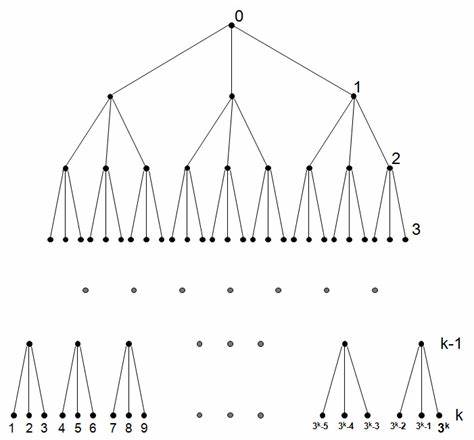
Die Welt der theoretischen Informatik ist geprägt von spannenden Konzepten und Modellen, die seit Jahrzehnten unser Verständnis von Berechnung und Computation formen. Eines der bekanntesten Modelle ist die Turing Maschine, die als ein idealisiertes, abstraktes Rechenmodell gilt. Doch höher hinaus über die Turing Maschinen hinaus, eröffnet das Konzept der Turing Bäume eine faszinierende und grafisch anschauliche Perspektive auf die Theorie der berechenbaren Funktionen, die neue Einblicke in den Kosmos der Computation bietet. Turing Bäume sind eine theoretische Konstruktion, die sich als unendliche, teilweise beschriftete vollständige binäre Bäume realisieren lassen. Jeder Knoten in einem solchen Baum wird durch eine endliche binäre Zeichenfolge eindeutig adressiert.
Das Besondere an Turing Bäumen ist, dass sie direkt computbare partielle Funktionen auf binären Zeichenfolgen kodieren. Im Gegensatz zu den traditionellen Programmcodes in der algorithmischen Informationstheorie, bei denen häufig nur prefixfreie Codes verwendet werden, erlauben Turing Bäume sogar Beschriftungen an inneren Knoten, was das Modell flexibler und universeller macht. Um den Zusammenhang besser zu verstehen, ist es hilfreich, bei der bekannten Turing Maschine zu beginnen. Eine Turing Maschine verarbeitet Eingabewörter aus einer binären Menge, verändert den Inhalt eines Bandes gemäß einer festgelegten Übergangsfunktion und kann nach einer endlichen Berechnung anhalten. Die Eingabe-Ausgabe-Beziehung der Maschine wird dabei als partielle Funktion zwischen binären Wörtern definiert, da die Maschine nicht auf jeder Eingabe unbedingt halten muss.
Die Idee bei Turing Bäumen besteht nun darin, für jede binäre Zeichenkette, die einen Knoten adressiert, die Ausgabe dieser Turing Maschine auf diese Zeichenkette als Beschriftung an genau diesem Knoten anzubringen – sofern die Maschine auf dieser Eingabe hält. Gibt es kein Haltverhalten, bleibt der Knoten unbeschriftet. Diese visuelle Abbildung einer Turing Maschine führt zu einem unendlichen Baum, der die möglichen funktionalen Eigenschaften der Maschine widerspiegelt. Dieser Blickwinkel ermöglicht nicht nur ein neues Verständnis der partiellen Funktionen, sondern auch eine elegante Darstellung der Komplexität und Verschachtelung von Berechnungen über Teilfunktionen hinweg. Eine besonders interessante Eigenschaft von Turing Bäumen ist, dass jeder Knoten im Baum selbst die Wurzel eines unendlichen Teilbaums ist, der wiederum eine vollständige binäre Baumstruktur mit Beschriftungen aufweist und somit auch ein Turing Baum ist.
Dadurch entsteht eine rekursive Struktur, in der sich jeder Teilbaum als eigenständige Repräsentation einer Turing Maschine verstehen lässt, die die ursprüngliche Maschine quasi „unterprogrammiert“. Das eröffnet Perspektiven auf Programmierung von Programmen, Simulationen von Funktionen und einen generellen Blick auf Komplexitätsschichten in der Berechenbarkeit. Die Verbindung zur Universalität, einem Kernstück der Berechenbarkeitstheorie, wird bei Turing Bäumen besonders deutlich. Eine universelle Turing Maschine hat die Fähigkeit, jede andere Turing Maschine zu simulieren. Entsprechend enthält der Turing Baum einer universellen Maschine alle anderen Turing Bäume als unendliche Teilbäume.
Der universelle Turing Baum bietet somit eine umfassende, alles einschließende Struktur, die als Panorama des gesamten Raums der berechenbaren partiellen Funktionen verstanden werden kann. Die Vorstellung aller Turing Bäume und ihrer Verschachtelungen miteinander zu verweben, wodurch isomorphe Teilbäume zusammenfallen, führt zum sogenannten Turing Netz. Dieses weitläufige Netzwerk ist ein unendlicher Graph, in dem jeder Knoten für einen Turing Baum steht und jeweils zwei gerichtete Kanten zu seinen ersten beiden Teilbäumen abgeht. Dieses Modell ermöglicht es, Programmierbarkeit und Emulation in einem topologischen Rahmen zu untersuchen. Die Struktur des Turing Netzes besitzt bemerkenswerte Eigenschaften.
So hat jeder Knoten genau zwei ausgehende Kanten, wohingegen die Eingangsgrade unendlich sind, was auf die vielen unterschiedlichen Arten verweist, wie ein gegebener Turing Baum als Teilbaum in größeren Turing Bäumen enthalten sein kann. Innerhalb des Netzes gibt es eine besonders wichtige Teilmenge, genannt die stark zusammenhängende Komponente der universellen Turing Bäume. Diese Komponente enthält alle universellen Bäume und ermöglicht Bewegungen zwischen beliebigen universellen Turing Bäumen, was die universelle Programmierbarkeit und Simulation ausdrückt. Jedoch ist zu beachten, dass das Turing Netz und die Turing Bäume theoretische Konstrukte sind, die nicht berechenbar sind. Die Berechnung der Beschriftung eines Knotens erfordert, dass man entscheiden kann, ob eine Turing Maschine auf einer bestimmten Eingabe hält, was bekanntlich das Halteproblem ist – und damit unlösbar.
Trotzdem bieten diese Konstruktionen ein mächtiges gedankliches Werkzeug zur Erfassung der gesamten Landschaft der berechenbaren Funktionen und deren komplexen Beziehungen untereinander. Durch den Einsatz von Turing Bäumen wird ein neues Fenster zur Welt der Computation aufgestoßen, das nicht nur funktionale Eigenschaften der Berechnung modelliert, sondern auch die zwischenhierarchischen Beziehungen und die programmatische Verschachtelung transparent macht. Diese Perspektive ist nicht nur für die theoretische Informatik spannend, sondern kann auch potenziell Anregungen für praktische Fragestellungen liefern, etwa im Bereich der formalen Verifikation, Komplexitätstheorie oder der Analyse von Programmsimulationen. Zusammenfassend lässt sich sagen, dass Turing Bäume ein elegantes und tiefgründiges Konzept darstellen, das die klassische Theorie der Turing Maschinen erweitert und visuell greifbar macht. Das daraus entstehende Turing Netz bildet eine universelle Netzwerkstruktur aller berechenbaren Funktionen ab und zeigt die umfangreichen Emulationsbeziehungen zwischen ihnen auf.
Obwohl in der Praxis aufgrund der Unentscheidbarkeit gewisse Einschränkungen bestehen, bleibt diese Sichtweise eine wertvolle theoretische Grundlage und eine Inspirationsquelle für weitere Forschungsarbeiten in der Informatik und Mathematik.