Die Theorie der Berechnungskomplexität ist ein Zweig der Informatik, der weit über die bloße Fähigkeit hinausgeht, ob eine Aufgabe lösbar ist, und stattdessen fokussiert, wie schwierig oder aufwendig es ist, diese Lösung zu erreichen. Während die klassische Berechenbarkeitstheorie seit den 1930er Jahren unser philosophisches Verständnis insbesondere in Bezug auf den Verstand und die Grenzen der Maschine geprägt hat, steht nun die Berechnungskomplexität im Zentrum einer potenziellen revolutionären Phase, die philosophische Debatten fundamental verändern wird. Diese Entwicklung findet vor allem durch die Arbeit und Überlegungen von Wissenschaftlern wie Scott Aaronson vom Massachusetts Institute of Technology (MIT) Aufmerksamkeit. Aaronson hebt hervor, dass es einen signifikanten Unterschied macht, ob ein Problem theoretisch lösbar ist oder praktisch in angemessener Zeit berechenbar – und dass diese Unterscheidung enorme Implikationen für die Philosophie haben kann. Berechnungskomplexität stellt die Frage, wie der Aufwand, eine Aufgabe zu lösen, in Abhängigkeit von der Größe des Problems wächst.
Klassisch betrachtet man “n” als Maß für die Problemgröße. Die Komplexitätsskala unterscheidet vor allem zwischen polynomieller Zeit, also einem Aufwand, der etwa mit n, n² oder anderen Potenzen von n wächst, und exponentieller Zeit, bei der etwa 2^n oder noch schnellere Wachstumsraten auftreten. Der Unterschied zwischen diesen beiden Kategorien ist gewaltig. Während Probleme mit polynomieller Zeit noch praktisch lösbar sind, übersteigt der Aufwand bei exponentiellem Wachstum oft jede vorstellbare Rechenkapazität – selbst wenn man der Leistung des Universums den Faktor Zeit hinzufügt. Für die Philosophie eröffnet das eine neue Dimension: Wenn eine Aufgabe zwar theoretisch lösbar, aber praktisch unlösbar ist, stellt dies die herkömmlichen Annahmen über Wissen, Erkenntnis und kognitive Fähigkeiten in Frage.
Ein eindrucksvolles Beispiel bietet die Debatte über künstliche Intelligenz und die Frage, ob Computer jemals wirklich wie Menschen denken können. Berühmt ist Roger Penrose’ Argument, dass Maschinen nicht in der Lage seien, die Konsistenz der formalen Systeme, auf denen sie basieren, zu «erfahren» oder zu «verstehen». Menschen hingegen besäßen diese Fähigkeit. Aaronson hingegen schlägt vor, die Diskussion neu zu führen und die Berechnungskomplexität zu betrachten. Ein Computer könnte prinzipiell eine extrem große Datentabelle mit allen möglichen Antworten auf all mögliche Fragen speichern – würde er so für alle denkbaren Gespräche die passende Antwort finden könnten, wäre er kaum von einem Menschen zu unterscheiden.
Doch dieser künstlich aufgeblasene Ansatz ist nicht nur unglaublich speicherintensiv, sondern auch exponentiell aufwendig in Bezug auf die Zeit und anderen Ressourcen. Das bedeutet, dass es praktisch unmöglich ist, diesen Weg zu gehen, auch wenn er theoretisch möglich ist. Das führt zu einer neue Sichtweise: Die fundamentale Grenze für Maschinenintelligenz ist nicht bloß die prinzipielle Berechenbarkeit, sondern vor allem die Komplexität der Berechnung. Die eigentliche Trennungslinie zwischen menschlichem Denken und maschineller Simulation könnte genau hier liegen – gerade weil Menschen mit erstaunlich effizienter Verarbeitung komplexer Informationen arbeiten. Die Betrachtung komplexitätstheoretischer Grenzen ermöglicht eine differenzierte Perspektive auf kognitive Prozesse und Erkenntnis, die über reine Funktionalität hinausgeht.
Die Relevanz der Berechnungskomplexität erstreckt sich aber nicht nur auf die künstliche Intelligenz. Auch die Philosophie der Mathematik wird davon tangiert. Nachdem jahrzehntelang der Formalismus oder Platonismus im Mittelpunkt standen, lenkt die Komplexitätstheorie die Aufmerksamkeit auf die praktische Zugänglichkeit mathematischer Erkenntnisse. Wenn gewisse mathematische Probleme zwar formal bewiesen werden könnten, aber die Verfahren dafür in exponentieller Zeit wachsen, stellt dies die Idee von „Wissen“ oder „Verstehen“ infrage. Es geht um die Zugänglichkeit der Wahrheit, um die Frage, ob Erkenntnis nur durch Beweisbarkeit reicht oder ob die Komplexität des Prozesses eine weitere Barriere bildet.
Auch in der Physik, speziell in der Quantenmechanik, wirft die Komplexitätstheorie neue Fragen auf. Quantencomputer versprechen eine Rechenleistung jenseits klassischer Maschinen und könnten einige komplexe Probleme in deutlich kürzerer Zeit lösen. Dadurch verändert sich das Verständnis der physikalischen Gesetzmäßigkeiten, wenn man Komplexität als eine grundlegende Eigenschaft der Wirklichkeit interpretiert. Die traditionelle Auffassung, dass alles in der Natur berechenbar ist, wird durch die Grenzen der praktischen Berechenbarkeit ergänzt – das eröffnet neue philosophische Betrachtungen über das Verhältnis von Natur, Wissen und Technologie. Trotz ihrer Potenziale ist die Berechnungskomplexität kein fertig entwickeltes Feld, sondern enthält Herausforderungen und offene Fragen.
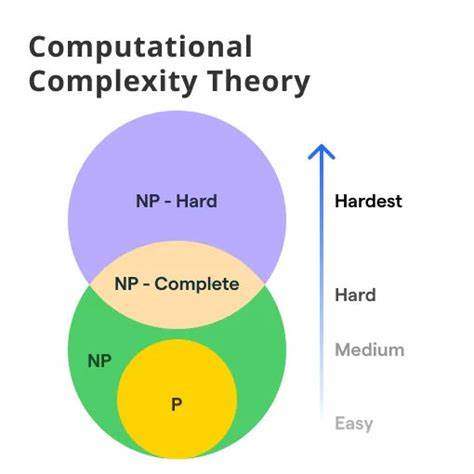
Zum Beispiel ist bis heute unbewiesen, ob die Klassen P und NP gleich sind oder nicht – eine der zentralen Fragen der Informatik mit tiefgreifenden Konsequenzen für Philosophie und Wissenschaft. Kritiker bemängeln auch, dass viele Modelle der Komplexitätstheorie auf idealisierten, deterministischen Rechenmaschinen beruhen, die von der Natur oder sogar menschlichem Denken abweichen. Dennoch bieten gerade diese Herausforderungen neue Denkanstöße für Philosophen, die sich mit Erkenntnistheorie und Wissenschaftstheorie beschäftigen. Die Berechnungskomplexität verdeutlicht, dass Wissen nicht nur eine Frage von Wahrheit ist, sondern auch von Aufwand, Zeit und Ressourcen. Sie verbindet technologische Erkenntnisse mit klassisch philosophischen Begriffen wie Erkenntnis, Intelligenz und Realität und zeigt, dass diese Begriffe vielschichtiger sind, als es traditionelle Betrachtungen vermuten ließen.
Zusammengefasst steht die computational complexity theory an der Schwelle, die Philosophie in den nächsten Jahren nachhaltig zu prägen. Sie erweitert den philosophischen Diskurs um eine Dimension, die technische Machbarkeit und Grenzen des Denkens und Wissens grundlegend miteinander verknüpft. Wer sich mit den Zukunftsfragen von Intelligenz, Erkenntnis und Realität auseinandersetzt, sollte die Einsichten der Berechnungskomplexität nicht nur kennen, sondern aktiv in die Diskussion einbeziehen. Darin steckt das Potenzial für eine neue philosophische Revolution, die unser Weltbild ebenso verändert wie die Technik selbst.