Die Erdős-Zahl ist ein Begriff, der tief in der Welt der Mathematik verwurzelt ist, doch ihr Einfluss geht weit über diesen Bereich hinaus in zahlreiche Wissenschaftsdisziplinen. Sie misst die kollaborative Distanz zwischen einem Forscher und dem berühmten ungarischen Mathematiker Paul Erdős, der im 20. Jahrhundert zu den produktivsten und aktivsten Mathematikern gehörte. Die Erdős-Zahl entstand als eine unterhaltsame und dabei gleichzeitig wissenschaftlich interessante Art und Weise, um die Vernetzung von Forschern anhand gemeinsamer Publikationen zu verfolgen. Dabei geht es nicht nur um rein mathematische Kooperationen, sondern auch um die interdisziplinären Brücken, die Forscher heute weltweit knüpfen.
Diese Zahl sind bei Wissenschaftlern nicht nur eine Art Statussymbol, sondern geben auch Aufschluss über die Kollaborationsstrukturen in der Forschung und ermöglichen es, Wissenschaft als ein großes Netzwerk aufzufassen. Paul Erdős galt als ein Ausnahmetalent und ein wandernder Geist der Mathematik. Er hatte keinen festen Wohnsitz, sondern reiste sein ganzes Leben lang von Universität zu Universität, um mit anderen Forschern zu arbeiten. In seiner Karriere veröffentlichte er mehr als 1.500 wissenschaftliche Arbeiten und arbeitete mit über 500 direkten Koautoren zusammen.
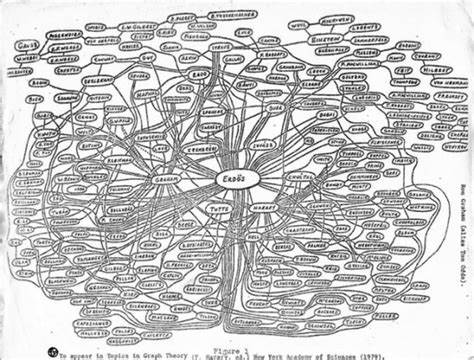
Diese außergewöhnliche Kollaborationsfreudigkeit führte dazu, dass sein Name zum Zentrum eines Kooperationsnetzwerks wurde, das in den letzten Jahrzehnten umfangreich untersucht wurde. Die Erdős-Zahl misst konkret die Distanz der Zusammenarbeit. Wer direkt mit Erdős zusammenarbeitete, besitzt die Erdős-Zahl 1, wer mit einem seiner Koautoren zusammenarbeitete, eine 2, und so weiter. Autoren, die keinen gemeinsamen Veröffentlichungsweg zu Erdős aufweisen, haben eine unendliche oder undefinierte Erdős-Zahl. Eine wichtige Rolle spielte die Erdős-Zahl auch bei der Analyse von Kooperationsnetzwerken.
Sie ist ein Paradebeispiel dafür, wie sich soziale und wissenschaftliche Verbindungen messen und graphisch darstellen lassen. Zusammengenommen lassen sich daraus Aussagen über die Wissenschaftsdynamik ableiten, beispielsweise wie sich neue Ideen verbreiten, wie oft Wissenschaftler zusammenarbeiten und wie Forschungsgebiete miteinander vernetzt sind. Mit der Zeit haben Mathematiker und andere Wissenschaftler erkannt, dass eine niedrige Erdős-Zahl eher eine Nähe zum Zentrum der fachlichen Gemeinschaft suggeriert und oft auch mit einem renommierten Forschungsumfeld einhergeht. Mittlerweile ist bekannt, dass die meisten Forscher eine Erdős-Zahl um 5 haben, wobei der Median bei etwa 5 liegt. Bedeutende Mathematiker wie Fields-Medaillengewinner haben oft eine wesentlich niedrigere Zahl, mit dem Median bei etwa 3.
Für neue Forscher ist es seit Paul Erdős’ Tod 1996 nicht mehr möglich, eine Erdős-Zahl von 1 zu erhalten, da sie nicht mehr direkt mit ihm zusammenarbeiten können. Dennoch kann man durch die vielfältigen Verbindungen zu den ehemaligen direkten Koautoren weiterhin niedrige Erdős-Zahlen erreichen. Berühmte historische Persönlichkeiten wie Srinivasa Ramanujan haben eine Erdős-Zahl von 3, obwohl sie zur Erdős-Zeit nicht aktiv zusammengearbeitet haben – dies ist möglich durch indirekte Verbindungspfade in der Veröffentlichungskette. Die Erdős-Zahl hat sich auch in anderen Wissenschaftsfeldern verbreitet. Naturwissenschaftler, Ökonomen, Philosophen und sogar Rechtswissenschaftler besitzen häufig eine Erdős-Zahl, da sie Forschungsarbeiten mit Mathematikern oder Forscherkooperationen über diverse Fächer hinweg eingingen.
Bekannte Nobelpreisträger der Physik und Wirtschaftswissenschaften besitzen beispielsweise Erdős-Zahlen im Bereich von 2 bis 6. In der Physik gibt es etliche Nobelpreisträger mit direkten oder indirekten Kooperationen zu Erdős, was die Überlappungen von physikalischer und mathematischer Forschung verdeutlicht. In der Ökonomie ist die Verbindung zwischen komplexer mathematischer Modellierung und wirtschaftlichem Fachwissen ebenfalls eng, sodass bekannte Wirtschafts-Nobelpreisträger eine Erdős-Zahl von 2 oder 3 besitzen können. Interessant ist auch die Rolle der Mathematiker in der Informatik und Kryptographie, deren Felder eine starke Grundlage in der diskreten Mathematik haben. Aus diesem Grund haben beliebte Kryptografen, die zum Beispiel das RSA-Verfahren erfunden haben, überschaubare Erdős-Zahlen, was die Verbreitung des Konzepts noch weiter bekräftigt.
In manchen Fällen ist sogar eine Verbindung in der Linguistik vorhanden, wie in der Arbeit von Noam Chomsky oder weiteren namhaften Wissenschaftlern, die mit Mathematikern kooperierten, wodurch bestimmte Sprachwissenschaftler ebenfalls eine Erdős-Zahl besitzen. Es gibt verschiedene Möglichkeiten, die Erdős-Zahl zu berechnen und zu definieren. Neben der klassischen Interpretation gibt es auch Variationen wie die „Erdős-Zahl zweiten Typs“, bei der nur Kooperationen mit genau zwei Autoren berücksichtigt werden. Dies schärft die Betrachtung bei der Analyse von Zusammenarbeit, da manche Arbeiten mit sehr vielen Mitautoren als weniger enge Kooperationsbeziehungen gelten können. Zudem wurden mathematisch orientierte Erweiterungen vorgeschlagen, um die „Nähe“ zu Erdős besser quantitativ zu erfassen.
So gibt es zum Beispiel Konzepte wie rationale Erdős-Zahlen, bei denen eine stärkere Zusammenarbeit mit Erdős tiefer gewichtet wird, oder elektrische Netzwerkanalysen, die den Widerstand zwischen Knotenpunkten im Kooperationsnetzwerk messen. Der Einfluss der Erdős-Zahl reicht auch in die Popkultur und interdisziplinäre Netzwerkspiele. Die Idee ähnelt dem „Six Degrees of Kevin Bacon“-Spiel, das die Kollaborationskette zwischen Schauspielern misst. Es entstand daraus das Konzept des Erdős-Bacon-Zahl, eine Kombination aus Erdős-Zahl und Bacon-Zahl, welches die Distanz einer Person zu Erdős im wissenschaftlichen Bereich und Kevin Bacon im Filmbereich kombiniert. Weiter wurden sogar Erdős-Bacon-Sabbath-Zahlen eingeführt, die auch die Verbindung zum Musikbereich berücksichtigen.
Solche spielerischen Ansätze erhöhen die öffentliche Aufmerksamkeit auf die Wichtigkeit von Vernetzung in Forschung und Kultur. Neben der numerischen Repräsentation von Zusammenarbeit vermittelt die Erdős-Zahl auch Einblicke in die Entwicklung der Wissenschaft selbst. In vergangenen Jahrhunderten war wissenschaftliche Kooperation weniger häufig und Veröffentlichungen erfolgten oft alleine. Die heutige Wissenschaft dagegen ist durch interdisziplinäre Zusammenarbeit und regelmäßige Koautorenschaften geprägt. Die Erdős-Zahlen spiegeln diese Entwicklung wider: Während frühere Forscher tendenziell höhere Erdős-Zahlen besitzen, sind es heutige Wissenschaftler mit ihrer intensiven Vernetzung, die meist deutlich niedrigere Erdős-Zahlen aufweisen.
Daraus wird der Wandel zu kollaborativer Forschung und die Entstehung eines globalen Wissenschaftsnetzwerkes deutlich. Wissenschaftliche Datenbanken und Werkzeuge, wie die vom American Mathematical Society angebotene Kollaborationsdistanzberechnung, erlauben Forschern und Interessierten, die Erdős-Zahl beliebiger Autoren abzufragen. Solche Tools nutzen umfangreiche Publikationsdatenbanken und zeigen die aktuellsten Verbindungen auf, wobei auch immer weiter verfeinerte Kriterien angewendet werden, um nur relevante gemeinsame Forschung zu berücksichtigen. Aufgrund der Vielzahl an Publikationen insbesondere bei Erdős und seinen direkten Koautoren, ist die Erdős-Zahl zu einem beliebten Maß für Netzwerkdichte und Verknüpfungsgrad in der mathematischen Forschung geworden. Abschließend lässt sich sagen, dass die Erdős-Zahl längst ein Symbol für die Bedeutung von Kooperation in der Wissenschaft ist.
Sie macht auf anschauliche Weise sichtbar, wie Forschung als ein dynamisches Netz von Individuen funktioniert, die gemeinsam neues Wissen erschaffen. Über Feld- und Ländergrenzen hinweg verbindet die Zahl Menschen und zeigt, wie aus der Zusammenarbeit vieler Einzelner bedeutende Fortschritte entstehen. Mit der fortschreitenden Digitalisierung und zunehmender Internationalisierung der Wissenschaft wird die Erdős-Zahl auch weiterhin eine Rolle spielen, um die Weite und Tiefe wissenschaftlicher Vernetzung zu messen und zu feiern.