In den letzten Jahren hat sich das Deep Learning zu einem der dynamischsten und erfolgreichsten Forschungsgebiete in der künstlichen Intelligenz entwickelt. Trotz des beachtlichen praktischen Erfolgs bleibt das theoretische Verständnis vieler Phänomene, die beim Training tiefer neuronaler Netzwerke auftreten, eine enorme Herausforderung. Das Neural Tangent Kernel (NTK) ist eine relativ neue theoretische Methode, die darauf abzielt, diese Komplexität zu durchdringen und die Trainingsdynamik von neuronalen Netzwerken besser zu verstehen. Dieses Konzept hat vor allem durch die Untersuchung von Netzwerken im sogenannten unendlichen Weiten-Limit (infinite-width limit) an Bedeutung gewonnen und bietet eine elegante Perspektive, wie sich komplexe nichtlineare Modelle verhalten, wenn ihre Architektur extrem groß wird. Das NTK stellt eine Verbindung zwischen neuronalen Netzwerken und Kernel-Methoden her, die bereits seit Jahrzehnten in der maschinellen Lernforschung verwendet werden.
Es handelt sich um einen mathematischen Kernel, der die Trainingsdynamik eines neuronalen Netzwerks innerhalb der Parameterraumentwicklung beschreibt. Durch die Einführung dieses Kerns lässt sich das Verhalten eines großen neuronalen Netzwerks in eine lineare Form übersetzen, was eine praxisnahe Analyse und sogar exakte Lösungen ermöglicht. Überraschenderweise zeigen Experimente, dass bei Netzwerken mit großer Breite die Gewichte während des Trainings kaum verändert werden, was als "Lazy Training" oder "gewichtslazy" Verhalten bezeichnet wird. Stattdessen lernt das Modell quasi nur durch eine lineare Approximation, die von diesem Kernel definiert wird. Eine einfache Möglichkeit, die Idee des NTK zu verstehen, besteht darin, sich ein neuronales Netzwerk mit nur einer Dimension als Eingabe und Ausgabe anzusehen.
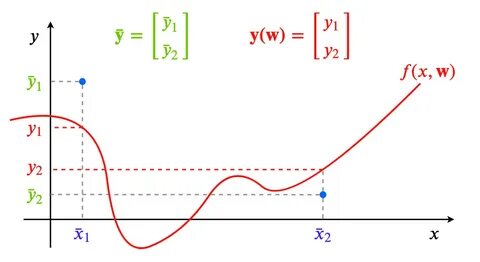
Nehmen wir an, ein kleines Netzwerk mit zwei versteckten Schichten und vielen einzeln aktivierten Neuronen wird zufällig initialisiert. Bei zunehmender Breite nähert sich die Verteilung der Funktionen, die dieses Netzwerk modellieren kann, zufälligen Proben aus einem Gaußschen Prozess an. In diesem Grenzfall lässt sich das gesamte Trainingsverhalten des Netzwerks durch lineare Modelle beschreiben, deren Parameter sich durch eine gewisse Kernel-Funktion charakterisieren lassen, eben das Neural Tangent Kernel. Das zentrale mathematische Werkzeug hierbei ist die Taylor-Entwicklung des Netzwerkoutputs um die Anfangsgewichte. Durch diese Linearisierung lässt sich die komplizierte, hochgradig nichtlineare Abbildung in eine lineare Funktion in Bezug auf die Parameter umwandeln.
So wird das ursprüngliche Problem der Optimierung von stark nichtlinearen Modellen auf ein lineares Regressionsproblem mit komplexen Features zurückgeführt. Diese Features sind durch die Gradienten des Netzwerkoutputs mit Bezug auf die Gewichte zum Initialisierungszeitpunkt gegeben. Die dabei entstehende Kernel-Matrix spiegelt dabei die inneren Produktstrukturen der Merkmalsabbildungen wider. Doch wann ist diese lineare Approximation sinnvoll? Die Qualität dieser Näherung hängt von der Größe der Veränderung der Gewichte ab, die während des Trainings auftritt. Für Modelle mit sehr großer Breite ist bekannt, dass die Gewichtsänderungen verschwindend klein sind.
Dadurch sind die Modelle im sogenannten Kernel-Regime, in dem sich das Netzwerk funktional kaum von seiner linearen Approximation unterscheidet. Forschungen zeigen, dass in dieser Regime das NTK während des gesamten Trainings nahezu konstant bleibt, was die Analyse der Trainingsdynamik stark vereinfacht. Sehr anschaulich lässt sich diese Beobachtung mit einem veränderten Skalierungsfaktor erklären. Indem man den Netzwerkoutput mit einer großen Zahl multipliziert, kann man das Modell gezielt in das Kernel-Regime zwingen. Dabei verschieben sich sowohl der Trainingsverlauf als auch die Optimallösung näher zum Ausgangspunkt der Gewichte, sodass sich das Verhalten immer mehr einem linearen Modell annähert.
Dieses Szenario wurde auch als "Lazy Training" bezeichnet, da die Gewichte im Training kaum verändert werden. Während die mathematischen Beweise für diese Eigenschaften komplex sind, beschreibt die zugrundeliegende Intuition eine sehr einfache Tatsache: Je mehr Neuronen ein Netzwerk hat, desto genauer kann eine kleine Änderung in vielen Gewichten große Veränderungen im Output bewirken. Daher müssen sich die Gewichte selbst nur wenig anpassen, um effektiv zu lernen. Dies erklärt, warum bei extrem breiten Netzwerken die Gewichtsänderungen minimal bleiben und die Linearisierung gilt. Die Dynamik, wie sich die Netzwerkparameter über die Trainingszeit verändern, kann mit dem Konzept des Gradient Flows modelliert werden.
Dies ist im Grunde genommen der kontinuierliche Grenzfall von diskreten Gradientenabstiegen mit unendlich kleinen Lernraten. In diesem Rahmen ergibt sich eine Differentialgleichung, die beschreibt, wie die Gewichte im Zeitverlauf auf den Abstieg des Fehlers reagieren. Unter der Annahme, dass der NTK während des Trainings unverändert bleibt, lässt sich das angepasst Modell direkt mit einer linearen Differentialgleichung beschreiben, deren Lösung eine Matrixexponentialfunktion ist. Dadurch lässt sich präzise vorhersagen, wie schnell und auf welche Weise das Modell die Trainingsdaten perfekt approximieren wird. Ein weiteres wichtiges Ergebnis ist, dass die Trainingsdynamik in diesem Kernel-Regime einem Lösungsprozess eines linearen Systems gleicht.
Diese Systeme sind überparametrisiert, was bedeutet, dass unendlich viele Lösungen existieren können. Die Eigenschaft des Gradientenabstiegs entscheidet hier, welche spezifische Lösung gewählt wird – nämlich diejenige mit minimaler Norm. Dies entspricht einer impliziten Regularisierung, die in der maschinellen Lernforschung als positiver Faktor für die Generalisierungsfähigkeit angesehen wird. Die generalisierende Wirkung des NTK lässt sich theoretisch durch die Verbindung zu reproduzierenden Kern-Hilberträumen (RKHS) beschreiben. Der NTK definiert eine spezifische Funktionalraum-Norm, deren Minimierung durch Gradient-Abstieg durchgeführt wird.
Dies schafft eine Brücke zwischen tiefen neuronalen Netzwerken und klassischen Kernel-Methoden, die seit langem für ihre guten Verallgemeinerungseigenschaften bekannt sind. Trotz all dieser vielversprechenden theoretischen Einblicke zeigen empirische Studien, dass das NTK-Regime nicht immer mit der tatsächlichen Leistung moderner neuronaler Netzwerke übereinstimmt. Brettstellung zeigen praktische Modelle häufig mehr dynamische Gewichtsänderungen und verlassen sich weniger auf eine lineare Approximation. Die Performance von reinen NTK-basierten Modellen liegt oft hinter der von echten trainierten Netzwerken zurück, insbesondere bei komplexen Datensätzen wie CIFAR-10 oder ImageNet. Aktuelle Forschungen versuchen, diese Diskrepanz durch verbesserte Kernel-Modelle oder alternative Theorien wie Mean-Field-Ansätze und optimalen Transport zu überbrücken.
Schließlich bietet das Konzept des Neural Tangent Kernel eine wertvolle Perspektive auf den Lernprozess in neuronalen Netzwerken. Es zeigt, dass trotz der inhärenten Nichtlinearitäten der Modelle und komplexen Trainingsprozesse ein großer Teil des Verhaltens durch eine lineare Approximation und Kernelfunktionen beschrieben werden kann. Dadurch lassen sich wichtige Fragen der Konvergenz, Stabilität und Überparametrisierung präzise angehen. Ein tiefergehendes Verständnis des NTK kann auch bei praktischen Anwendungen helfen, indem es Einblicke in die Sensitivität verschiedener Modelparameter und die Rolle der Initialisierung im Trainingsprozess liefert. So können beispielsweise Modelle gezielt skaliert werden, um das „Lazy Training“ zu vermeiden oder zu fördern, je nachdem, welche Eigenschaften für die jeweilige Anwendung gewünscht sind.
Die ständige Weiterentwicklung der Theorie rund um das Neural Tangent Kernel und seine Verknüpfungen mit anderen mathematischen Konzepten wird voraussichtlich auch in Zukunft eine Schlüsselrolle bei der Erklärung und Verbesserung neuronaler Netzwerke spielen. Für Forschende und Praktiker bietet das NTK somit einen faszinierenden Ansatzpunkt, um die Komplexität moderner Deep-Learning-Modelle durch mathematische Klarheit besser zu begreifen und in die Praxis zu übertragen.