Eigenwerte und Eigenvektoren gehören zu den zentralen Konzepten der linearen Algebra und finden in zahlreichen wissenschaftlichen und technischen Bereichen Anwendung. Trotz ihrer weitreichenden Bedeutung bleiben sie oft abstrakt und schwer verständlich. Eine visuelle Herangehensweise kann dabei helfen, diese Konzepte intuitiv zu erfassen und ihre Wichtigkeit besser zu begreifen. Der folgende Text erklärt diese Begriffe detailliert und veranschaulicht sie durch praxisnahe Beispiele, die zeigen, wie sie in realen Systemen wirken. Zunächst beschreibt man einen Vektor als eine Größe mit Richtung und Länge im zweidimensionalen Raum, dargestellt durch einen Punkt oder einen Pfeil mit Koordinaten.
Eine Matrix hingegen kann man sich als eine Art Regel vorstellen, die jeden Vektor auf eine bestimmte Weise verändert, indem sie ihn in eine neue Richtung lenkt und eventuell seine Länge verändert. Wenn man einen Vektor v mit der Matrix A multipliziert, erhält man einen neuen Vektor Av. Im Allgemeinen verändert eine Matrix jeden Vektor auf unterschiedliche Weise. Es gibt jedoch spezielle Vektoren, sogenannte Eigenvektoren, die bei der Multiplikation mit der Matrix A lediglich in ihrer Länge skaliert, aber nicht in ihrer Richtung verändert werden. Das heißt, wenn Av gleich λ mal v ist, wobei λ eine reelle oder komplexe Zahl ist, dann ist v ein Eigenvektor und λ der zugehörige Eigenwert.
Dies kann man sich bildlich so vorstellen, dass A den Vektor v entlang seiner Linie streckt oder staucht, jedoch nicht dreht. Eigenvektoren bilden sogenannte Eigenspaces – Linien, auf denen alle Vektoren bei Multiplikation mit A lediglich skaliert werden. Die Skalierungsfaktoren sind die entsprechenden Eigenwerte. Je nachdem, ob der Eigenwert größer, kleiner oder gleich eins ist, des Dehnungs- oder Stauchverhalten der Matrix entsprechend. Liegt der Eigenwert unter eins, zieht A den Vektor näher zum Ursprung, bei einem Eigenwert größer als eins wird der Vektor gestreckt und entfernt sich vom Ursprung.
Dies ist besonders wichtig, um zu verstehen, wie Systeme sich über wiederholte Anwendung einer Matrix entwickeln. Betrachtet man die wiederholte Anwendung einer Matrix A auf einen Anfangsvektor v, spricht man von der Bildung einer Vektorsequenz v, Av, A²v, und so weiter. Ein zentrales Ergebnis der modernen linearen Algebra ist, dass diese Sequenzen durch die Eigenvektoren und Eigenwerte entscheidend beeinflusst werden. Dabei fungieren die Eigenvektoren als Richtungsgeber, während die Eigenwerte das Wachstum oder die Abnahme der Vektoren in diesen Richtungen steuern. Somit gibt das Studium der Eigenwerte und Eigenvektoren wertvolle Hinweise darauf, wie sich ein dynamisches System mit der Zeit verhält.
Diese Erkenntnisse sind nicht nur abstrakt, sondern haben vielfältige praktische Anwendung. Ein klassisches Beispiel ist die Beschreibung der Fibonacci-Folge mittels eines dynamischen Systems. Hier stellt man sich eine Population von zwei Gruppen vor – etwa Kinder und Erwachsene, deren Veränderungen von einem Moment zum nächsten durch eine Matrix beschrieben werden. Die Matrix kodiert dabei die Wachstums- oder Umwandlungsregeln zwischen den Gruppen. Durch wiederholte Anwendung der Matrix entstehen Zahlenfolgen, die den berühmten Fibonacci-Zahlen entsprechen.
Diese Zahlen wachsen asymptotisch und konvergieren in Richtung eines Eigenvektors, dessen Eigenwert den Wachstumsfaktor angibt. Dies ist ein anschauliches Beispiel dafür, wie natürliche Wachstumsprozesse durch lineare Transformationen und ihre Eigenwerte modelliert werden können. Ein weiteres spannendes Anwendungsfeld findet sich bei Markov-Ketten und den sogenannten Markov-Matrizen. Diese Matrizen beschreiben Systeme, in denen ein Zustand durch Wahrscheinlichkeiten auf andere Zustände übergeht, beispielsweise die Wanderungsbewegung von Menschen zwischen zwei Städten. Hierbei hat die Matrix stets Eigenschaft, dass alle Elemente positiv sind und die Spaltensummen jeweils eins betragen.
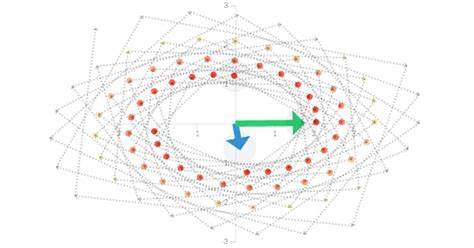
Dies garantiert, dass ein Eigenwert von genau eins existiert und dass das System mit der Zeit auf einen stabilen Zustand zuläuft – den sogenannten stationären Zustand. Dieser ist ein Eigenvektor, der durch den Eigenwert eins skaliert wird, was bedeutet, dass sich das System im Gleichgewicht befindet und sich nicht mehr verändert. Solche Konzepte sind essenziell für die Modellierung in Bevölkerungsdynamiken, Ökonomie und sogar in Suchalgorithmen wie Googles PageRank. Dazu kommen komplexe Eigenwerte und Eigenvektoren, die in Systemen auftreten können, die Schwingungen oder Drehbewegungen beinhalten. Wenn Eigenwerte einen Imaginärteil besitzen, entstehen bei wiederholter Anwendung der Matrix Spiralmuster in der Entwicklung der Vektoren.
Diese Drehung um den Ursprung ist charakteristisch für viele physikalische Systeme, wie etwa elektrische Schaltkreise oder mechanische Schwingungen. Durch eine Visualisierung dieser komplexen Eigenwerte als Punkte in der komplexen Zahlenebene lässt sich die dynamische Entwicklung anschaulich nachvollziehen. Unabhängig von der Anfangsbedingung erzeugt die Matrix dabei eine typische Spiralbewegung im Vektorraum. Das Verständnis von Eigenwerten und Eigenvektoren geht weit über einfache mathematische Übung hinaus. Sie sind fundamentale Werkzeuge, um komplexe Systeme zu analysieren, dynamische Prozesse zu beschreiben und Vorhersagen zu treffen.
Sei es in der Physik, der Biologie, Informatik oder Wirtschaft, fast überall findet man Fälle, in denen lineare Transformationen eine Rolle spielen und deren Eigenpaare entscheidend sind. Für das tiefergehende Studium dieser Themen empfehlen sich renommierte Lernressourcen wie der Linear Algebra Kurs von Gilbert Strang am MIT, der zahlreiche Anwendungen und das theoretische Fundament behandelt. Auch Kurse zur Differenzialgleichung ergänzen das Wissen sinnvoll, insbesondere da viele zeitabhängige Systeme sowohl mit Eigenwerten als auch mit Ableitungen beschrieben werden. Zusammengefasst bietet die visuelle Betrachtung von Eigenwerten und Eigenvektoren einen intuitiven Zugang zu komplexen mathematischen Konzepten. Durch die Darstellung von Vektoren als Pfeile im Raum und der Betrachtung ihrer Transformation durch Matrizen werden Zusammenhänge verständlich und nachvollziehbar.
Die unterschiedlichen Anwendungen von der Fibonacci-Folge über Bevölkerungsmodelle bis hin zu Drehbewegungen zeigen, wie universell diese Ideen genutzt werden können. Das macht sie zu einem unverzichtbaren Werkzeug für Wissenschaft, Technik und Datenanalyse in der modernen Welt.