Warum Sie diese Matrix nicht invertieren sollten: Effiziente Methoden zur Lösung von linearen Gleichungssystemen

In der linearen Algebra und bei der Lösung von Gleichungssystemen trifft man häufig auf die Gleichung Ax=b, wobei A eine quadratische Matrix und x sowie b Vektoren sind. Eine allgemeine Herangehensweise, die oft theoretisch diskutiert wird, ist die Berechnung der Inversen von A, um anschließend durch Multiplikation mit b die Lösung x zu bestimmen. Obwohl diese Methode auf den ersten Blick intuitiv erscheint, wird sie von Experten der numerischen Linearen Algebra häufig als ineffizient und potenziell fehleranfällig kritisiert. Der Ratschlag „Invertiere die Matrix nicht“ ist deshalb in vielen Lehrbüchern und wissenschaftlichen Diskussionen präsent, doch nur wenige gehen in ihren Erklärungen darauf ein, warum das so ist und wann es wirklich relevant wird. Um diese Thematik umfassend zu verstehen, lohnt sich ein genauerer Blick auf die mathematischen Verfahren, die hinter der Berechnung von x stehen, und die Grenzen, die mit der expliziten Inversion einer Matrix verbunden sind.

Ein zentrales Werkzeug zur Lösung solcher linearen Gleichungssysteme ist die LU-Zerlegung, benannt nach der unteren (Lower) und oberen (Upper) Dreiecksmatrix, in die eine gegebene Matrix A faktorisierbar ist. Bei der LU-Zerlegung wird A durch sukzessive Gaußsche Eliminationsschritte in eine Produktform gebracht, bei der die linke Matrix L eine untere Dreiecksmatrix ist und U eine obere Dreiecksmatrix. Die Umwandlung ist ökonomisch und ermöglicht es, das Gleichungssystem in zwei einfach zu lösende Teilprobleme zu zerlegen: zuerst wird das Zwischenprodukt y aus Ly=b durch Vorwärtseinsetzen berechnet, anschließend wird x aus Ux=y durch Rückwärtseinsetzen gelöst. Diese zwei Schritte sind drastisch rechenintensiv günstiger als die vollständige Berechnung von A⁻¹, da sie die Struktur der Dreiecksmatrizen ausnutzen, deren Gleichungssysteme mit minimalem Rechenaufwand lösbar sind. Vergleicht man die Komplexität der Operationen, so wird klar, dass die LU-Zerlegung in etwa O(n³) Operationen benötigt, während das Lösen des Gleichungssystems über Vorwärts- und Rückwärtseinsetzen hingegen nur O(n²) flops beansprucht.

Die berechnete Inverse verlangt hingegen eine deutlich höhere Anzahl von Fließkommaoperationen: Um die gesamte Inverse zu bestimmen, müssen n Gleichungssysteme mit n Dimension gelöst werden, was insgesamt etwa drei Mal so teuer ist wie das direkte Lösen eines einzelnen Systems. Zusätzlich ist nach der Inversion noch eine Matrix-Multiplikation mit dem Vektor b notwendig, die ebenfalls O(n³) Operationen beansprucht. Insgesamt summieren sich Aufwand und mögliche Fehlerquellen dadurch erheblich. Ein weiterer entscheidender Grund, warum explizites Invertieren meist nicht ratsam ist, liegt in der numerischen Stabilität. Die Inversion einer Matrix verstärkt tendenziell Fehler, die aufgrund von Rundungen und numerischen Ungenauigkeiten entstehen können.

Diese Problematik wird vor allem bei schlecht konditionierten Matrizen sichtbar, bei denen der sogenannte Konditionszahlwert sehr hoch ist. Die Konditionszahl einer Matrix misst dabei, wie sensitiv die Lösung des Systems auf kleine Änderungen in den Eingangsdaten reagiert. Eine hohe Konditionszahl deutet darauf hin, dass schon geringfügige Störungen zu großen Abweichungen im Ergebnis führen können. Da bei der Inversion auch mit der Berechnung von A⁻¹ selbst ein Fehlerterm multipliziert wird, können sich Ungenauigkeiten im Ergebnis bei Multiplikation mit b stark verstärken, was in praktischen Anwendungen katastrophale Folgen haben kann. Hingegen führt das direkte Lösen des Systems durch LU-Zerlegung mit nachgeschalteten Vorwärts- und Rückwärtseinsetzen in der Regel zu wesentlich kleineren Fehlern, da hierbei die Fehlerpropagation kontrollierter ist.

Das Konzept von Vorwärts- und Rückwärtseinsetzen bei Dreiecksmatrizen hilft zusätzlich bei der effizienten Lösung. Die untere Dreiecksmatrix L hat auf der Diagonalen Einsen stehen, was bedeutet, dass man nacheinander die einzelnen Komponenten von y relativ einfach bestimmen kann, indem man immer nur die bereits berechneten Werte nutzt. Danach erlaubt die obere Dreiecksmatrix U, in umgekehrter Reihenfolge ebenfalls schnell das Ergebnis für x zu bestimmen. Diese schrittweise lineare Substitution ist sowohl speicher- als auch rechenzeiteffizient und vermeidet unnötige Matrixoperationen. Zudem versprechen Bibliotheken für numerische Lineare Algebra wie LAPACK oder Eigen höchste Optimierung dieser Verfahren für eine breite Palette von Anwendungen.

Ein naheliegendes Argument für die Nutzung der Inversion könnte der Wunsch sein, die Lösung x für unterschiedliche rechte Seiten b mehrfach zu berechnen. In solchen Fällen kann man tatsächlich von einer Vorberechnung der Inversen profitieren, doch praktische Erfahrung und viele Quellen aus der Mathematik zeigen, dass selbst dann andere Verfahren, etwa die Faktorisierung durch LU oder QR, vorzuziehen sind, da sie eine bessere Numerik gewährleisten und weniger Rechenkosten verursachen. Zudem bieten iterative Lösungsverfahren oder speziell zugeschnittene Algorithmen weitere Alternativen, die bei sehr großen und dünnbesetzten Matrizen die direkte Inversion weit hinter sich lassen. Neben der Rechengeschwindigkeit und der Genauigkeit spielt auch der Aspekt der Lesbarkeit und des Verständnisses in der Programmierung eine Rolle. Wer direkt die Funktion zur Lösung von linearen Gleichungen nutzt, zeigt klar die Intention des Codes, nämlich das Problem Ax=b effizient zu lösen.

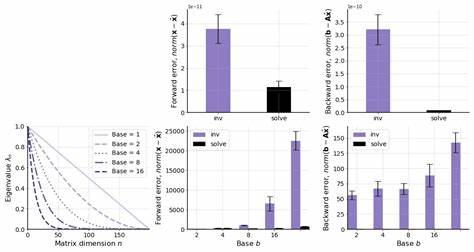
Das explizite Berechnen von A⁻¹ und anschließendes Multiplizieren erzeugt zusätzliche Zwischenschritte und kann anfälliger für Fehler sein, vor allem wenn nicht klar ist, wie die Inverse berechnet wurde. Die Wartbarkeit und Sicherheit des Codes profitieren also ebenfalls von der direkten Lösungsstrategie. Zahlreiche numerische Experimente bestätigen diese theoretischen Vorteile eindrucksvoll. Durch Vergleiche von Laufzeiten zeigt sich klar, dass das direkte Lösen von linearen Gleichungssystemen mit wachsender Matrixgröße immer bevorzugt wird. Dieses Ergebnis kann für kleine Matrizen kaum bedeutsam erscheinen, doch im Zeitalter von Big Data, Machine Learning und großdimensionierter Simulationen sind Einsparungen im Rechenaufwand von Faktor drei oder mehr höchst signifikant.

Zudem verdeutlichen Tests mit gut- und schlecht konditionierten Matrizen, dass die Genauigkeit der Ergebnisvektoren bei Invertierung bei schlechten Konditionen der Eingangsmatrix stark beeinträchtigt sein kann. Im Gegensatz dazu bleiben die Resultate bei direktem Lösen häufig deutlich stabiler und zuverlässiger. Abgesehen von den rein mathematischen und rechentechnischen Argumenten ist es außerdem hilfreich, das allgemeine Prinzip der numerischen Stabilität und Konditionierung zu verstehen. Das numerische Lösen eines Problems ist immer mit Approximationen verbunden, da in digitalen Computern nur endliche Präzision zur Verfügung steht. Die Idee der Vorwärts- und Rückwärtsfehleranalyse hilft dabei, abzuschätzen, wie groß die Abweichungen zwischen exakter und berechneter Lösung sind und wie sich diese Abweichungen zusammensetzen.

Eine direkte Inversion verschlechtert häufig die Rückwärtsfehler, wodurch die Nähe zur tatsächlichen Lösung schlechter wird. Bei Systemen mit guten Konditionseigenschaften mögen sich die Unterschiede in der Genauigkeit dagegen eher gering halten, dennoch ist die Verwendung der Inversion auch in solchen Fällen meist unnötig kompliziert. Nicht zuletzt stellt die praktische Implementierung von Algorithmen in Bibliotheken wie NumPy, MATLAB oder SciPy sicher, dass für das Lösen von Ax=b meist genau die effizienteren und stabileren Methoden genutzt werden. Funktionen wie np.linalg.

solve umgehen die Inversion explizit und verwenden stattdessen optimierte Faktorisierungen. Wenn Programmierer dennoch auf np.linalg.inv setzen, tun sie dies häufig aus Gewohnheit oder Unkenntnis und riskieren dadurch unnötige Laufzeitverluste und Ungenauigkeiten. Abschließend lässt sich festhalten, dass das Motto „Invertiere nicht die Matrix“ keinesfalls nur eine theoretische Weisheit darstellen, sondern in der Praxis durch klare Vorteile untermauert wird.

Wer lineare Gleichungssysteme effizient und verlässlich lösen möchte, sollte sich mit den mathematischen Grundlagen der LU-Zerlegung und der Vorwärts- sowie Rückwärtssubstitution auseinandersetzen und moderne Algorithmen nutzen. Neben der verbesserten Rechenzeit und Genauigkeit wird so auch der Umgang mit numerischen Ungenauigkeiten und potenziell schlecht konditionierten Problemen verbessert. Die Matrixinversion bleibt dagegen als Operation wichtig für spezielle Anwendungen, etwa bei analytischen Herleitungen oder theoretischen Untersuchungen, sollte aber im Alltag der numerischen linearen Algebra als Werkzeug zum Lösen von Gleichungssystemen im Hintergrund bleiben.