Signierte Abstandsfunktionen (SDFs) und effiziente Algorithmen zu ihrer Berechnung gewinnen zunehmend an Bedeutung in vielen Bereichen der Computergraphik, Simulation und maschinellen Lernens. Die Fähigkeit, ein Objekt oder dessen Rand durch eine implizite Funktion auf einem diskreten Gitter präzise und performant zu beschreiben, eröffnet neue Möglichkeiten in der Rekonstruktion, Modellierung und Visualisierung komplexer Geometrien. Ein entscheidendes mathematisches Werkzeug für die Berechnung von Abstandsfunktionen ist die Lösung der Eikonal-Gleichung, und das Fast Sweeping Verfahren stellt dabei eine besonders effiziente Methode dar. Diese Betrachtung widmet sich eingehend den theoretischen Hintergründen der Eikonal-Gleichung, dem Fast Sweeping Algorithmus, dessen Umsetzung in der Programmiersprache JAX sowie der praktischen Anwendung und deren Leistungsvorteilen gegenüber traditionellen Methoden. Zunächst ist es wichtig, das Konzept der signierten Abstandsfunktion zu verstehen.
Fundamentale Idee ist, dass eine Fläche oder ein Volumen im Raum durch eine Funktion beschrieben wird, deren Nullstelle genau die Grenzfläche repräsentiert. Das heißt, für Punkte auf der Oberfläche ist der Funktionswert null, für Punkte innerhalb des Volumens negative Werte und für Punkte außerhalb positive Werte – oder umgekehrt, je nach Definition. Dadurch lässt sich das Objekt implizit in einem Raster darstellen, ohne die explizite Speicherung der Geometrie. Diese Repräsentation ist insbesondere bei der Modellierung deformierbarer Objekte oder bei der Simulation von Frontausbreitung hilfreich. Die Berechnung dieser Funktionen erfolgt oft über die Eikonal-Gleichung, eine nichtlineare partielle Differentialgleichung vom Typ hyperbolischer Gleichung, die vielfältige physikalische und geometrische Situationen modellieren kann.
Allgemein drückt sie den Zusammenhang zwischen der Gradientenlänge einer Funktion, hier der Ankunftszeit eines sich ausbreitenden Fronts, und einer Geschwindigkeit ausdrückt, die das Ausbreitungstempo bestimmt. Anschauungsbeispiel ist eine Flamme, die von einem Feuer ausgeht und über eine Fläche verteilt fortschreitet. Die Ankunftszeit an jedem Punkt ist dann umso größer, je weiter der Punkt von der Ausgangsstelle entfernt ist, wobei Hindernisse und unterschiedliche Geschwindigkeiten berücksichtigt werden können. Traditionelle numerische Verfahren zur Lösung der Eikonal-Gleichung, etwa durch klassische Diskretisierung und Integration, stoßen oft an Grenzen, insbesondere wenn Singulärstellen oder sogenannte Schocks auftreten. Solche Stellen entstehen, wenn sich Fronten überlagern oder sich Geometrien verändern, und herkömmliche Methoden liefern dann meist ungenaue oder instabile Lösungen.
Genau hier setzt das Fast Sweeping Verfahren an. Es wurde als effiziente Methode entwickelt, um eine stabile und schnelle Näherung der Lösung zu berechnen, insbesondere in Anwendungen mit komplexer Geometrie maschinellen und physikalischen Problemen. Das Fast Sweeping Verfahren zeichnet sich durch seinen iterativen Charakter aus, bei dem das Gitter in zyklischen Richtungen durchlaufen wird. Dabei aktualisiert der Algorithmus die Werte an jeder Stelle anhand der Nachbarwerte, die den Informationsfluss aus bestimmten Richtungen widerspiegeln. In zwei Dimensionen bedeutet das, dass alle vier Kombinationen von Richtungsbewegungen durchlaufen werden, um sicherzustellen, dass Ausbreitungsinformationen aus allen quadranten übernommen werden.
Gerade die Berücksichtigung der sogenannten upwind- Differenzen, eine spezifische Diskretisierung im Sinne der Strömungsrichtung, ist dabei essenziell für korrekte und konsistente Ergebnisse. Ein praktisches Problem bei der Umsetzung auf dem Computer ist die effiziente Verwaltung der Randbedingungen und der bekannten beziehungsweise festen Wertequellen, welche die Fronten definieren. Im Algorithmus werden Quellen und Hindernisse als sogenannte „frozen cells“ markiert, diese werden während der Berechnung nicht verändert, um eine korrekte Ausgangsbasis für die sich ausbreitende Lösung zu bilden. Das durchdachte Padding mit großen Werten sorgt zudem für eine saubere Behandlung der Gitterränder und verhindert unerwünschte Grenzartefakte. Die theoretisch elegante und algorithmisch optimale Lösungskonzeptualisierung wurde in der Praxis durch Python-Bibliotheken und Frameworks umgesetzt, wobei JAX als moderne Bibliothek besonders sticht.
JAX kombiniert NumPys Benutzerfreundlichkeit mit fortschrittlichem automatischem Differenzieren und JIT-Kompilierung für GPU- und TPU-Beschleunigung. Somit eröffnet sich die Möglichkeit, das Fast Sweeping Verfahren nicht nur verständlich, sondern auch performant zu implementieren. Die Verwendung von JAX erlaubt es, Schleifen und Aggregationen optimal für die Parallelisierung vorzubereiten und gleichzeitig übersichtlichen, reproduzierbaren Code zu schreiben. Im Kern der JAX-Implementierung steht die Erzeugung von schnellen, kompilierbaren Routinen, welche die wiederholten Sweeps effizient abarbeiten. Dabei werden klassische Python-Schleifen mit JAX-für-Schleifen substituiert, was das explizite Tracen der Rechenströme für den Compiler möglich macht.
JAXs vmap und lax.fori_loop werden genutzt, um Indizes über die Gitterdimensionen elegant zu iterieren und parallel auszuführen. Solche Features sind in reinem NumPy nicht verfügbar oder nur mit Zusatzaufwand zu realisieren. Der Quellcode zeigt, wie sich die bekannten Schleifenstrukturen in eine funktionale, JIT-kompilierte Form übersetzen lassen. Das ist besonders für iterative Verfahren wie das Fast Sweeping Verfahren von großem Vorteil, da viele Durchläufe auf einem möglichst großen Gitter schnell ausgeführt werden müssen.
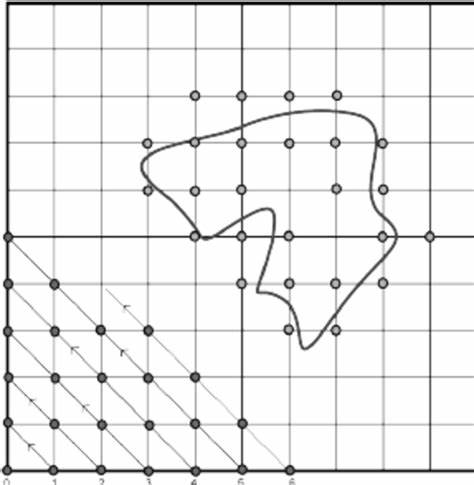
Neben der reinen Rechenzeit ist die Visualisierung der Resultate ein wichtiger Aspekt im Umgang mit Interface-Propagation-Problemen. Im vorgestellten Beispiel werden komplexe Formen wie „Bohnen-“ähnliche Umrisse sowie Hindernisse im Gitter definiert, um realistische Anwendungsszenarien abzubilden. Die erzeugte Distanzfunktion wird in Form von Konturlinien dargestellt, welche die Ausbreitung der Front über die Zeit hinweg anschaulich machen. Die Möglichkeit, die Visualisierungen interaktiv über Parameter wie Iterationszahl und Gitterauflösung zu verändern, erleichtert das Verständnis der dynamischen Prozesse hinter der Methode erheblich. Interessant ist auch die Praxisrelevanz der Leistungsvorteile bei der Verwendung von JAX gegenüber reinem NumPy-Code.
Benchmark-Ergebnisse demonstrieren eine deutliche Beschleunigung, insbesondere auf modernen CPUs wie Apple M2 Pro. Obwohl spezialisierte C++-basierte Bibliotheken wie skfmm in puncto Speed unvergleichlich sind, bieten Python-Implementierungen mit JAX ein hervorragendes Gleichgewicht zwischen Performance, Flexibilität und Benutzerfreundlichkeit. Gerade für Forscher und Entwickler, die Algorithmen schnell anpassen und experimentell erweitern wollen, ist dieser Vorteil nicht zu unterschätzen. Ein weiterführender Aspekt betrifft die parallelisierte Version des Fast Sweeping Verfahrens. Optimierungen und Weiterentwicklungen der Methode versuchen, die inherent sequenzielle Abfolge der Sweeps zu überwinden und mehrere Richtungen simultan zu berechnen.
In der Praxis stößt man hierbei insbesondere in JAX aufgrund von statisch definierten Compiler-Constraints auf Herausforderungen. Eingriffsweisen wie das parallele Anwenden der Sweeps und anschließende Zusammenführen mittels Elementweise-Minimierung sind theoretisch einfach, lassen sich aber in der aktuellen Technologieumgebung nur schwer effizient abstrahieren. Aktuelle Forschung und Community-Feedback könnten hier in naher Zukunft Lösungen hervorbringen, welche den Rechenprozess noch effektiver und skalierbarer gestalten. Zusammenfassend bietet das Fast Sweeping Verfahren in Kombination mit moderner Software wie JAX eine leistungsfähige Methode zur Berechnung von signierten Abstandsfunktionen. Der algorithmische Ansatz setzt auf ein schnelles, iteratives Upwind-Schema, welches die Informationen über mehrere Richtungen verteilt und so stabile und zuverlässige Näherungen liefert.