Der Kalman-Filter ist eine leistungsstarke Methode zur Schätzung des Zustands eines dynamischen Systems in Gegenwart von Rauschen und Unsicherheiten. Ursprünglich in den 1960er Jahren von Rudolf E. Kalman entwickelt, hat sich der Kalman-Filter zu einem unverzichtbaren Werkzeug in vielen Bereichen wie der Robotik, Signalverarbeitung, Navigation und Wirtschaftswissenschaften entwickelt. Die Stärke des Kalman-Filters liegt in seiner Fähigkeit, auf elegante Weise Vorhersagen und Messungen zu kombinieren, um so eine optimale Schätzung des Systemzustands zu erhalten. Dieses Verständnis soll durch eine einfache Herleitung und Erklärung der zugrunde liegenden Prinzipien erleichtert werden.
Das Grundprinzip des Kalman-Filters basiert darauf, einen unbekannten Zustand kontinuierlich anhand von verrauschten Messungen zu schätzen. Ein dynamisches System kann durch Zustandsvariablen beschrieben werden, deren Entwicklung über die Zeit durch eine sogenannte Zustandsdynamik bestimmt wird. Dabei sind Messungen des Systems meist unvollständig und fehlerbehaftet. Ziel des Filters ist es, die beste Schätzung dieses Zustands durch Berücksichtigung der Systemmodelle, der Messungen sowie der Unsicherheiten zu erreichen.Eine optimale Schätzung im Sinne des Kalman-Filters bedeutet die Minimierung des mittleren quadratischen Fehlers zwischen dem geschätzten und dem tatsächlichen Zustand.
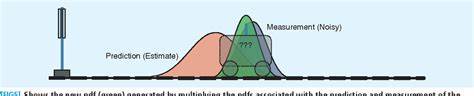
Hierbei spielt die Wahrscheinlichkeitsrechnung eine fundamentale Rolle: Der Filter arbeitet mit den sogenannten Zustandswahrscheinlichkeitsverteilungen, welche die Unsicherheit über den Systemzustand ausdrücken. Das Verfahren vereint zwei wesentliche Schritte: die Vorhersage und die Aktualisierung. In der Vorhersage wird auf Basis des bisherigen Zustands und des Modells eine Prognose für den neuen Zustand erstellt. Die Aktualisierung nutzt die neu eingegangene Messung, um diese Prognose zu korrigieren und die Schätzung zu verbessern.Die mathematische Formulierung beginnt mit der Annahme eines linearen Modells, welches den Übergang des Systemzustands über die Zeit beschreibt, sowie einem Messmodell, das definiert, wie Beobachtungen aus den Zuständen erzeugt werden.
Dabei gehen wir von Gaußschem Rauschen sowohl in der Zustandsentwicklung als auch in den Messungen aus. Dies erlaubt eine geschlossene Form der Wahrscheinlichkeitsverteilungen, nämlich die Normalverteilung. Im Detail beschreibt eine Zustandsübergangsgleichung den neuen Zustand als lineare Kombination des vorherigen Zustands und eines Steuervektors, addiert um ein stochastisches Rauschen. Analog ist die Messung eine lineare Abbildung des wahren Zustands, ebenfalls mit einem Messrauschen behaftet.Um den Filter formal herzuleiten, wird die Bayessche Statistik verwendet.
Die bedingte Verteilung des aktuellen Zustands anhand aller bisherigen Messungen wird schrittweise aktualisiert. Zunächst erfolgt die Vorhersage des Zustandsprior mithilfe der Zustandsübergangsfunktion. Im nächsten Schritt wird der sogenannte Innovationsvektor berechnet, der die Differenz zwischen der tatsächlichen Messung und der Vorhersage der Messung darstellt. Dieser Unterschied wird gewichtet mittels einer Kalman-Verstärkung, einem Koeffizienten, der die Unsicherheit der Vorhersage und Messung in Relation setzt, und dient zur Korrektur der Zustandsvorhersage.Der Kalman-Filter besitzt mehrere attraktive Eigenschaften.
Er ist rekursiv, was bedeutet, dass keine Historie aller Messergebnisse benötigt wird, sondern lediglich die letzte Schätzung und die aktuelle Messung berücksichtigt werden. Dadurch reduziert sich der Speicher- und Rechenaufwand erheblich. Außerdem kann er nahezu optimal sein unter der Annahme linearer Systeme mit Gaußschem Rauschen. In realen Anwendungen werden Erweiterungen wie der erweiterte Kalman-Filter (EKF) oder der Unscented Kalman-Filter (UKF) verwendet, um nichtlineare Systeme zu berücksichtigen.Die Anwendung des Kalman-Filters reicht von der Flugobjektverfolgung über Fahrzeugnavigation bis hin zur Wirtschaftsanalyse.
Besonders in der Robotik ermöglicht er die präzise Positionsbestimmung trotz unvollständiger oder verrauschter Sensorinformationen. Auch in der Finanzwelt hilft er bei der Modellierung und Prognose von Zeitreihen, indem er interne Zustände wie Trends und Schwankungen schätzt.Das intuitive Verständnis des Kalman-Filters lässt sich durch das Bild eines Fehlers schonenden Mittelwertfilters beschreiben. Während in einfachen Filtern Messwerte lediglich gemittelt werden, balanciert der Kalman-Filter die Unsicherheiten von Modellvorhersage und Messung gewichtet aus. Eine präzise Modellierung der Systemdynamik und der Rauschstatistiken ist daher essentiell für die Effizienz des Filters.
Die einfache Herleitung des Kalman-Filters zeigt, dass es sich im Kern um ein zweistufiges Verfahren handelt: Im ersten Schritt wird die Information aus dem letzten Schätzwert und dem Systemmodell vorweggenommen, im zweiten Schritt wird diese Prognose mittels der aktuellen Messung verbessert. Damit existiert ein stetiger Kreislauf der Schätzung, der stark rauschbehaftete Messungen ausgleicht und so eine robuste Zustandsbestimmung erlaubt.Zusammenfassend lässt sich sagen, dass der Kalman-Filter durch seine mathematisch fundierte Vorgehensweise eine effiziente Methode zur Zustandschätzung in dynamischen Systemen darstellt. Seine Basis ist klar strukturiert auf der Kombination von Vorhersage und Korrektur, basierend auf Wahrscheinlichkeiten und linearen Modellen. Die einfache Herleitung fördert das Verständnis, wie verschiedene Komponenten zusammenwirken: Zustandsschätzung, Messung, Unsicherheit und Korrektur.
Für jeden, der sich mit Signalverarbeitung, Steuerung oder statistischer Schätzung beschäftigt, bietet der Kalman-Filter eine fundamentale und vielseitige Technik, die unverzichtbar für moderne technische und wissenschaftliche Anwendungen ist.