Die abc-Vermutung gehört zu den bekanntesten und gleichzeitig rätselhaftesten offenen Problemen in der modernen Zahlentheorie. Seit ihrer Formulierung in den 1980er-Jahren haben zahlreiche Mathematiker versucht, sie entweder vollständig zu beweisen oder zumindest signifikante Teilergebnisse zu erzielen. Die Vermutung verbindet fundamentale Eigenschaften von Zahlen, insbesondere das sogenannte Radikal einer Zahl, mit Gleichungen der Form a + b = c. Trotz intensiver Forschungsarbeit bleibt die Vermutung in ihrem allgemeinsten Sinne unbewiesen. Doch jüngste Entwicklungen insbesondere im Bereich der automatisierten Beweisführung und Formalisierung bringen frischen Wind in die Diskussion und liefern überzeugende Ergebnisse, die zeigen, dass die abc-Vermutung für einen Großteil der möglichen Tripel gilt.
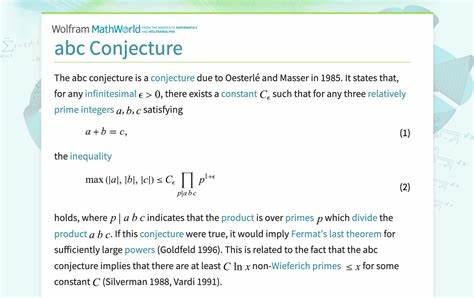
Diese Erkenntnis wird oft als „abc-Vermutung fast immer wahr“ bezeichnet und stellt einen bedeutenden Fortschritt dar. Im Kern besagt die abc-Vermutung, dass für drei positive, teilerfremde ganze Zahlen a, b und c, die die Gleichung a + b = c erfüllen, eine wichtige Beziehung zwischen dem Produkt der verschiedenen Primfaktoren von abc und der Größe der Zahl c existiert. Genauer geht es dabei um das Radikal von abc, das definiert ist als das Produkt aller verschiedenen Primfaktoren von a, b und c. Die Vermutung behauptet, dass das Radikal in gewisser Weise eng mit der Größe von c verbunden ist und dass das Produkt der Primfaktoren im Normalfall mindestens ungefähr so groß ist wie c hoch (1-ε) für beliebig kleines positives ε. Was macht die abc-Vermutung so faszinierend? Zum einen verbindet sie das additive und das multiplikative Verhalten von Zahlen auf elegante Weise.
Zum anderen hat sie erstaunliche Konsequenzen für viele andere Vermutungen und Theoreme in der Zahlentheorie, beispielsweise für Fermats letzten Satz, die Verteilung von Primzahlen und für Diophantische Gleichungen allgemein. Ein Nachweis der abc-Vermutung würde direkt zu einer Vielzahl weiterer Ergebnisse führen und viele offene Fragen in der Zahlentheorie auflösen. Trotz dieser Relevanz ist der allgemeine Beweis der abc-Vermutung äußerst schwierig. In der Vergangenheit gab es immer wieder viel diskutierte Beweisversuche, wie den von Shinichi Mochizuki durch Operative Inter-Universal Teichmüller Theory, dessen Komplexität selbst Experten vor fast unüberwindbare Hürden stellt. Daher gewinnt die Suche nach alternativen Zugängen, etwa durch automatisierte Formalisierung von Teilresultaten, an Bedeutung.
Eine solche neuartige Methode ist die automatisierte Formalisierung, bei der Beweise nicht nur menschlich formuliert, sondern von einem Computersystem nachvollziehbar und prüfbar dargestellt werden. Hier kommt das Programm Trinity des Unternehmens Morph Labs ins Spiel. Diese Software erstellt maschinell formale Beweise, die über eine strenge Sprache vom System Lean verifiziert werden können. In einem beeindruckenden Projekt wurde mit Trinity eine Teilversion der abc-Vermutung formalisiert, die unter dem Titel „Die abc-Vermutung fast immer wahr“ bekannt ist. Der bemerkenswerte Aspekt dabei ist, dass nicht die gesamte allgemeine Vermutung formalisiert wurde, sondern eine Resultat der klassischen Mathematiker de Bruijn, die das Ausmaß der Ausnahmen zur abc-Vermutung präzise quantifiziert.
Konkret konnte gezeigt werden, dass die Menge derjenigen Tripel (a, b, c), bei denen die abc-Vermutung nicht zutrifft, in einem Intervall bis N nur etwa in der Größenordnung von N hoch zwei Drittel existiert. Dies bedeutet, dass die Ausnahmefälle verglichen mit allen möglichen Tripeln verschwinden, je größer das Intervall betrachtet wird. Anders gesagt: Für die überwiegende Mehrheit der Zahlen ist die abc-Vermutung tatsächlich wahr. Durch die Formalisierung werden nicht nur die Resultate verifiziert, sondern die Wahrscheinlichkeit von Fehlern im Beweis drastisch reduziert. Dies unterstreicht auch die hohe Bedeutung automatisierter Systeme für die Zukunft der Mathematik.
Aufwändige komplexe Beweise, die Menschen nur schwer vollständig nachvollziehen können, werden für eine maschinelle Prüfung zugänglich gemacht und damit eine neue Ebene der Vertrauenswürdigkeit erreicht. Die Umsetzung erfolgte mit dem Beweissystem Lean, das speziell entwickelt wurde, um intuitive mathematische Sachverhalte in eine formale und für Computer verständliche Sprache zu übersetzen. Mithilfe von Trinity wurden alle notwendigen Schritte, einzelne Lemmas, Hintergrundannahmen und Beweisketten maschinell generiert und in Lean ausgeführt. Das Resultat ist ein vollständig verifizierter maschineller Beweis, der einen bedeutenden Teilaspekt der abc-Vermutung absichert. Neben dem rein mathematischen Fortschritt bringt die Arbeit aus dem Morph Labs Projekt auch wichtige Impulse für Zukunft und Anwendung der automatisierten Beweistheorie.
Gerade bei großen, komplexen Vermutungen mit vielschichtigen Strukturen bietet sich diese Methode an, um Teilstücke und Zwischenergebnisse völlig neu und absolut sicher zu überprüfen. Zudem eröffnet sich dadurch die Möglichkeit, das Verständnis für tiefe mathematische Zusammenhänge zu erweitern und das Vertrauen in den Stand der Beweise zu erhöhen. Darüber hinaus hat das formale Verifizieren gerade in der akademischen Welt eine zunehmende Bedeutung. Wissenschaftliche Ergebnisse sollen reproduzierbar und sicher sein. Insbesondere im Bereich der reinen Mathematik ist dies essenziell, da ein falsch verstandener oder unvollständiger Beweis gravierende Auswirkungen auf zahlreiche weitere Arbeiten haben kann.
Automatisierte Formalisierungen schaffen genau hier einen Paradigmenwechsel und ergänzen die menschliche Forschung um eine maschinell gesicherte Grundlage. Parallel dazu wird die Anzahl der bekannten Formalisierungen von klassischen Theoremen stetig größer. Dies zeigt, wie sich die Mathematik weg von reinem Papierbeweis hin zur digitalen Prüfung entwickelt. Die abc-Vermutung fast immer wahr kann dabei als Meilenstein angesehen werden, welcher die Verbindung zwischen traditioneller Zahlentheorie und moderner Technologie symbolisiert. Nicht zuletzt stellt sich die Frage, wie die weitere Zukunft der abc-Vermutung aussehen wird.
Während ein vollständiger Beweis möglicherweise noch auf sich warten lässt, profitieren Forscher und Mathematiker bereits jetzt von der Gewissheit, dass ein Großteil der Vermutung korrekt ist. Ebenso können automatisierte Beweiser eine Grundlage für zukünftige Versuche bieten, die Vermutung endgültig zu lösen. Insgesamt ist die erfolgreiche automatisierte Formalisierung eines so tiefgreifenden Ergebnisses wie der fast immer gültigen abc-Vermutung eine bemerkenswerte Leistung, die weit über den engeren Fachkreis hinaus Beachtung findet. Sie verbindet mathematische Eleganz mit technologischem Fortschritt und zeigt, dass die Zusammenarbeit von Mensch und Maschine in der Wissenschaft neue Türen öffnet. Die Entwicklung rund um die abc-Vermutung und ihre automatisierte Beweisführung ist somit nicht nur ein triumphaler Moment in der Zahlentheorie, sondern auch ein Ausblick auf die Zukunft der Forschung insgesamt.
Die Integration von maschinellen Hilfen wird die Art und Weise verändern, wie Mathematik betrieben wird, und möglicherweise die Lösung großer Geheimnisse der Zahlenwelt noch greifbarer machen.