In der heutigen Welt des Game Designs sind Zahlen überall – ob offen sichtbar für Spieler oder unbemerkt im Hintergrund steuernd. Gleich ob Stärke, Schaden, Erfahrungspunkte oder Schwierigkeitsgrad: Hinter jedem dieser Werte stehen mathematische Funktionen, welche die Wechselwirkungen und Fortschritte der Spielmechaniken regeln. Für Entwickler und Designer ist es essenziell, die richtigen Funktionen einzusetzen, um Systeme zu gestalten, die sowohl balanciert als auch eingängig sind. Die Wahl der mathematischen Funktion beeinflusst, wie sich ein Spieler aufsteigend fühlt, wie schnell Herausforderungen wachsen oder wie lohnend Belohnungen erscheinen. Während viele Funktionen ihre Wurzeln in der Mathematik haben, liegt die Kunst darin, sie so einzusetzen, dass sie das Spielerlebnis organisch unterstützen und für den Spieler nachvollziehbar bleiben.
Erste Überlegungen führen oft zu linearen Funktionen. Sie sind einfach, intuitiv und lassen sich leicht berechnen. Eine lineare Funktion beschreibt eine gleichmäßige Zunahme oder Abnahme eines Wertes, was das Verständnis für den Spieler erleichtert. Wenn zum Beispiel die Kampfstärke eines Charakters proportional zu dessen Level steigt, dann ist eine lineare Skalierung passend. Der Spieler kann sofort abschätzen, wie sich das Aufleveln auf seine Stärke auswirkt.
Dieses Gefühl von Klarheit ist wertvoll in Systemen, in denen Transparenz gewünscht wird. Allerdings stößt die Linearität bei komplexeren Anforderungen schnell an ihre Grenzen. Viele Spiele wollen nicht nur einfache Steigerungen abbilden, sondern auch dynamische Progressionen, bei denen Anfangsgewinne spürbar höher sind oder Herausforderungen exponentiell zunehmen. Hier kommen Potenzfunktionen ins Spiel. Potenzfunktionen, etwa quadratische oder kubische, erzeugen immer stärkere Steigerungen, sobald der Eingabewert wächst.
Sie bulgen innerhalb des Bereichs zwischen null und eins nach unten und schaffen dadurch interessante Effekte in Animationen oder Geschwindigkeitseinstellungen. Besonders bei wachsender Zahl jenseits von eins bieten sie einen natürlichen Weg zur Beschleunigung von Werten, was Spieler das Gefühl von wachsender Macht vermitteln kann. Die Balance bleibt dabei jedoch kritisch. Sind sowohl Schadenswerte als auch gegnerische Lebenspunkte potenziell exponentiell wachsend, kann das Spiel schnell aus dem Gleichgewicht geraten. Umso wichtiger ist es, das Verhältnis der verschiedenen Funktionen zueinander zu betrachten.
Die Kombination unterschiedlicher Skalierungen wirkt sich unmittelbar auf das Spielerlebnis aus. Beispielhaft steigen in einem RPG eventuell Questbelohnungen quadratisch, Verbrauchsgegenstände bleiben stabil, Ausrüstungspreise wachsen linear, während Ausrüstungskosten für das Charakterumgestalten sogar kubisch wachsen. Für Spieler bedeutet dies, dass größere Mengen an Verbrauchsgegenständen einfacher verfügbar sind, während die Ausrüstung im Vergleich wertvoller wird und besonders das Umgestalten des Charakters mit steigendem Fortschritt zur Herausforderung wird. Feinjustierungen gelingen durch den Einsatz von Potenzen mit Bruchzahlen. Funktionen mit Exponenten zwischen null und eins erzeugen eine Art abnehmenden Grenznutzen – je mehr man einen Wert steigert, desto geringer wird der zusätzliche Effekt.
Das ist etwa nützlich bei Schadensreduktion durch Ausrüstung: Die erste Resistenz bringt viel, weitere Items nur noch wenig zusätzlichen Schutz. Solche Funktionen front-loaden die Wirkung und verhindern eine Überladung durch powervolle Stapelungen. Im Gegensatz dazu stehen negative Potenzen, die invers zum Wert wirken. Sie sind besonders sinnvoll, um Effekte mit abnehmender Wirkung durch mehrfaches Stapeln zu modellieren. So können negative Effekte, wie Verzögerungen oder Debuffs, eingearbeitet werden, die nach dem ersten Stapel stark wirken, danach aber in ihrer Wirkung abschwächen.
Ein weiterer essenzieller Funktionstyp ist das exponentielle Wachstum. Hier nimmt der Wert nicht nur stetig zu, sondern wächst immer schneller, da die Steigerung proportional zum aktuellen Wert ist. Exponentielle Funktionen eignen sich für Systeme, in denen das Wachstum dramatisch und ungebremst dargestellt werden soll. Beispielhaft sind Idle Spiele, in denen Zahlenexplosion das zentrale Spielerlebnis prägen. Perzeptiv erzeugen solche Funktionen ein Gefühl steter Machtzunahme bei konstanten Prozentsteigerungen von Stufe zu Stufe.
Die Möglichkeit, mit verschiedenen Basen zu arbeiten, lässt die Kurve von sanften Anstiegen bis zu rasanten Explosionen variieren. Neben dem exponentiellen Wachstum existiert die exponentielle Abnahme. Hier nähert sich der Wert asymptotisch einem Grenzwert, häufig null, und modelliert nützlich abklingende Effekte oder schwindende Boni. So kann ein Schadensfaktor mit zunehmender Entfernung abnehmen, ohne abrupt zu verschwinden, was realistisch und intuitiv wirkt. Die Bedeutung spezieller Zahlenfolgen wie der Dreieckszahlen veranschaulicht, wie spielerisch einfach bestimmte Kosten- oder Fortschrittssysteme sein können.
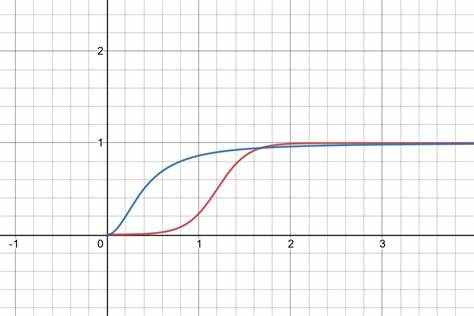
Dreieckszahlen entstehen, wenn man die Summe aller Zahlen von eins bis n betrachtet – eine Funktion, die sich hervorragend zur Bestimmung von Aufwandswerten eignet, die mit jedem Level oder Upgrade steigen. In vielen Rollenspielen basieren Erfahrungspunkte- oder Upgrade-Systeme auf diesem Prinzip, weil es eine natürlich ansteigende, aber gut nachvollziehbare Progression darstellt. Schließlich sind Sigmoidfunktionen ein faszinierendes Werkzeug für Designer, die Systeme mit klaren Grenzen und abflachenden Verstärkungen suchen. Sigmoide Kurven, erkennbar an ihrer S-Form, steigen zu Beginn steil an und nähern sich am Ende einem maximalen Wert an. Die bekanntesten Vertreter sind die logistische Funktion und die algebraische Sigmoidfunktion.
Die logistische Funktion ist dank klar definierter Parameter wie Steilheit, Obergrenze und Versatz einzigartig anpassbar. Dadurch lassen sich beispielsweise Schadensabfälle über Distanz oder Geschwindigkeitsboni je nach Zeit einfach modellieren. Ihre symmetrische Form sorgt für eine gleichmäßige Steigung, die sich gut in balancierte Spielmechaniken integrieren lässt. Die algebraische Sigmoidfunktion ist von Natur aus asymmetrisch, was bedeutet, dass die Wirkung einer Steigerung früher stärker ausfällt und später langsamer abflacht. Das kann nützlich sein, wenn erste Verbesserungen besonders spürbar sein sollen, während spätere Schübe sanfter verlaufen.
Sigmoide sind auch favorable Optionen für Systeme mit Caps, denn sie begrenzen Werte zuverlässig und sorgen so für eine geschmeidige Begrenzung ohne harte Grenzen, die das Spielerlebnis stören könnten. Insgesamt eröffnet der gezielte Einsatz dieser unterschiedlichen mathematischen Funktionen vielfältige Möglichkeiten im Spieldesign. Das Zusammenspiel von linearen, potenzbasierten, exponentiellen und sigmoiden Funktionen erlaubt es, Progressionen maßgeschneidert zu gestalten und dem Spiel eine typische „Gefühlsdynamik“ zu verleihen. Ob man schnelle Steigerungen, sanfte Caps, abnehmende Erträge oder dramatische Wachstumsphasen abbilden möchte – in jedem Fall sind diese mathematischen Werkzeuge keineswegs nur Zahlen, sondern ein essenzieller Teil des Spielerlebnisses. Für Systemdesigner ist es ratsam, stets die Verhältnisse der verschiedenen Funktionen im Blick zu behalten – denn erst die Kombination macht einen gut balancierten und spannenden Spielfortschritt aus.
Dabei gilt es, sowohl die technischen Aspekte im Hinterkopf zu behalten als auch die Wahrnehmung und Erfahrungen der Spieler. Ein transparentes, nachvollziehbares System ermöglicht Optimierung und Motivation, während ein zu komplexes oder intransparente Algorithmus Spieler frustrieren kann. Ebenso spielt auch die Performance eine Rolle: Lineare Operationen sind schnell und einfach, während komplexe Potenzen und Divisionen mehr Rechenleistung erfordern, was in Echtzeit- oder ressourcenbegrenzten Szenarien bedacht werden muss. Letztlich sind diese mathematischen Funktionen mehr als die Summe ihrer Variablen und Koeffizienten. Sie sind Werkzeuge zur Gestaltung von Spielerfahrung, Motivation und Balance.
Das Verständnis ihrer Eigenschaften und ihres Zusammenspiels eröffnet Designer wertvolle Möglichkeiten für das Entwerfen von Systemen, die nicht nur funktional, sondern auch emotional wirksam sind. Die Welt der mathematischen Funktionen für Spielsysteme ist weitreichend, komplex und gleichzeitig spannend in ihren Anwendungsmöglichkeiten. Wer die Prinzipien hinter ihnen versteht und kreativ einsetzt, verfügt über einen entscheidenden Vorteil bei der Entwicklung anspruchsvoller, mitreißender Spielewelten.