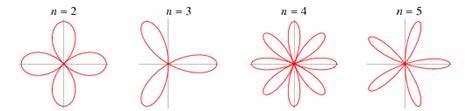
Rosen zählen seit jeher zu den schönsten und beliebtesten Blumen weltweit. Ihre zarten Blütenblätter mit charakteristischen spitzen Rändern und kunstvollen Wölbungen sind nicht nur ein Sinnbild für Schönheit, sondern auch ein Beispiel für komplexe natürliche Prozesse, die ihr Wachstum und ihre Form steuern. Während viele Aspekte von Pflanzenwachstum gut erforscht sind, enthüllt eine aktuelle Studie einen bislang unbekannten mathematischen Mechanismus, der Rosenblätter prägt – eine ungewöhnliche Art von geometrischem Feedback, die in der Natur bisher nie beobachtet wurde. Die Form von Rosenblättern ist weit mehr als ein ästhetisches Merkmal. Sie beeinflussen die Bestäubung, Schutz vor Umwelteinflüssen und spielen eine Rolle bei der optimalen Nutzung von Licht und Wasser.
Traditionell wurde angenommen, dass das Wachstum von Pflanzenblättern durch genetische Steuerung und biochemische Signale bestimmt wird. Doch die Forschergruppe um Zhang, Cohen, Moshe und Sharon hat in einer aktuellen Veröffentlichung, die im renommierten Magazin Science erschienen ist, einen neuen Blick auf diese Entwicklung geworfen und dabei mechanische sowie mathematische Prinzipien in den Fokus gerückt. Im Kern ihrer Entdeckung steht ein spezifischer Wachstumsprozess, bei dem die Rose ihre Blätter nicht einfach flach ausbildet, sondern durch eine dynamische Interaktion zwischen Wachstum und mechanischem Stress besondere Formen generiert. Mit Hilfe theoretischer Analysen, Computermodellen und Experimenten mit künstlichen, elastischen Materialien wie gummiartigen Plastikbögen konnten die Wissenschaftler nachweisen, wie ein mechanisches Feedback die Entstehung der spitzen und gerollten Blattränder steuert. Das Besondere an diesem Feedbackmechanismus ist, dass er sich von herkömmlichen biologischen Steuerungen unterscheidet.
Während klassische Modelle davon ausgehen, dass Wachstum vorgegeben und einfach abläuft, zeigt diese Studie, dass das Wachstum im Rosenblatt durch die Krümmung und Spannungen im Blatt selbst reguliert wird. Wenn sich die äußeren Ränder des Blattes nach außen wölben, erzeugt die dabei entstehende mechanische Spannung ein Signal, das wiederum das Wachstum in diesen Bereichen beeinflusst. Durch diese Rückkopplung entsteht eine selbsterhaltende Schleife, die spitze Blattränder und charakteristische Kurven formt. Die mechanische Rückkopplung ist dabei ungewöhnlich, weil sie auf geometrischen Prinzipien der Oberflächenkrümmung beruht. Ähnlich wie bei einem gekrümmten Stück Papier oder einem gebogenen Glas erzeugt die Form der Oberfläche Kräfte, die das Material verändern.
Im Falle der Rosenblätter wird so das Wachstum lokalisierter Bereiche gezielt verstärkt oder gehemmt, was die komplexe Blattform begünstigt. Diese Erkenntnisse eröffnen neue Möglichkeiten für das Verständnis von Pflanzenwachstum und Entwicklung. Indem sie mechanische Aspekte und geometrische Mathematik integrieren, zeigen die Forscher Wege auf, wie komplexe biologische Formen entstehen, ohne dass dafür allein komplizierte genetische Programme notwendig sind. Stattdessen entsteht Struktur auch durch physikalische Prozesse, die sich über einfache Rückkopplungen selbst organisieren. Ein weiterer spannender Aspekt der Studie ist die Verwendung von künstlichen Materialien, um den Wachstumsprozess nachzuahmen.
Durch Experimente mit flexibel gedehnten Plastikblättern konnten die Wissenschaftler die theoretischen Vorhersagen eindrucksvoll bestätigen und sogar neue Hypothesen für weitere Forschungen generieren. Solche biomimetischen Ansätze, die Naturphänomene technisch nachbilden, sind immer häufiger Quelle für Innovationen in der Materialwissenschaft und Technik. Die Bedeutung dieser Forschung reicht weit über die botanische Welt hinaus. Das Verständnis, wie mechanische Kräfte biologische Wachstumsprozesse beeinflussen, kann beispielsweise dabei helfen, besser zu verstehen, wie sich Gewebe im menschlichen Körper entwickeln oder wie sich natürliche Strukturen im Laufe der Evolution angepasst haben. Die Anwendungen könnten von der regenerativen Medizin bis zur Entwicklung neuer, flexibler Werkstoffe in der Technik reichen.
Auch aus mathematischer Sicht ist die Entdeckung bemerkenswert. Die Art des mechanischen Feedbacks, das hier beobachtet wurde, stellt eine neue Form der geometrischen Rückkopplung dar, die bislang in der Natur noch nicht dokumentiert war. Dies zeigt, wie eng Mathematik und Naturwissenschaft miteinander verknüpft sind und wie mathematische Modelle als Schlüssel dienen können, um natürliche Phänomene besser zu verstehen. Zusammengefasst lässt sich sagen, dass die Form der Rosenblätter ein Produkt eines faszinierenden Zusammenspiels aus Wachstum, mechanischem Stress und geometrischer Krümmung ist. Durch die Identifikation dieses ungewöhnlichen mathematischen Mechanismus wurde ein neues Kapitel in der Erforschung komplexer biologischer Formen eröffnet.