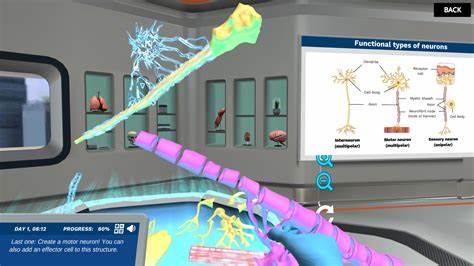
Die Erforschung virtueller Neuronen ist ein faszinierender Bereich der Computational Neuroscience, der Einblicke in das komplexe Verhalten von Nervenzellen ermöglicht. Während das Gehirn Milliarden von echten Neuronen enthält, versuchen Wissenschaftler durch Simulationen auf Computern, das Verhalten einzelner Nervenzellen virtuell abzubilden. Der Aufbau eines solchen virtuellen Neurons erfordert ein feines Zusammenspiel biologischer Erkenntnisse und mathematischer Modelle. Besonders das Hodgkin-Huxley-Modell hat sich als fundamentale Grundlage in diesem Bereich etabliert. Es ist bis heute eines der elegantesten und biologisch realistischsten Modelle zur Beschreibung von Aktionspotenzialen, also den elektrischen Signalen, die Neuronen zur Informationsübertragung nutzen.
Ein tieferes Verständnis dieses Modells ermöglicht nicht nur die Simulation von neuronaler Aktivität, sondern auch die Untersuchung verschiedener neurophysiologischer Phänomene und die Entwicklung von Anwendungen in Neurowissenschaft und Medizin. Zu Beginn ist es entscheidend zu verstehen, was genau ein virtuelles Neuron darstellen und bewirken soll. Die Frage, wie detailliert die Simulation sein muss, ist von großer Bedeutung. Wäre es möglich, alle Proteine, Ionenarten und deren Interaktionen bis ins kleinste Detail nachzubilden? Zwar klingt das theoretisch reizvoll, aber in der Praxis führt eine solche Komplexität oft dazu, dass man weder das biologische System noch die Simulation selbst noch verlässlich versteht. Außerdem stellen die notwendigen Rechenressourcen eine massive Hürde dar.
Daher muss man sich bewusst entscheiden, welchen Aspekt des neuronalen Verhaltens man modellieren möchte und welche Ebenen der Details funktional weggelassen werden können. Für ein neuronales Modell, das Aktionspotenziale produziert und das Zusammenspiel von Natrium- und Kaliumionen berücksichtigt, bietet sich das Hodgkin-Huxley-Modell an. Das Hodgkin-Huxley-Modell beruht auf experimentellen Messungen an Riesenaxonen von Tintenfischen aus den frühen 1950er Jahren. Die Forscher Alan Hodgkin und Andrew Huxley beschrieben erstmals quantitativ, wie Ionen durch die Zellmembran eines Neurons fließen und wie daraus das Aktionspotenzial entsteht. Das Modell basiert auf der Analogie des Neurons mit einem elektrischen Schaltkreis: Die Zellmembran verhält sich wie ein Kondensator, der elektrische Ladung speichert, während die Ionenkanäle als variable Widerstände oder Leitfähigkeiten fungieren.
Unterschiedliche Ionenarten, vor allem Natrium und Kalium, werden durch sogenannte Gleichspannungsquellen repräsentiert, die das Bestreben der Ionen darstellen, sich entsprechend ihrer Konzentrations- und elektrischen Gradienten zu bewegen. Ein wesentliches Element des Modells ist die Membrankapazität, die es erlaubt, den zeitlichen Verlauf der Spannung an der Zellmembran in Abhängigkeit von den einfließenden oder ausfließenden Ionenströmen zu beschreiben. Auf diese Weise wird die Änderung der Membranpotentials – also die elektrische Spannung zwischen Innen- und Außenseite der Membran – mit Differentialgleichungen präzise festgelegt. Zu Beginn eines Aktionspotenzials ist die Membran meist auf einem Ruhepotential von etwa -65 Millivolt. Dies resultiert aus einer Kombination von Ionenverhalten: Die Konzentration von Natrium ist außerhalb der Zelle höher als innerhalb, während Kalium im Inneren in höherer Konzentration zu finden ist.
Die Membran selbst ist jedoch für Ionen normalerweise undurchlässig, sodass sich ein Ladungsgefälle aufbauen kann. In der Simulation öffnet sich zu Beginn das Natriumtor langsam, bis es plötzlich schnell und nahezu vollständig öffnet – ein Verhalten, das im Modell durch sogenannte Öffnungsvariablen beschrieben wird, die die Wahrscheinlichkeit darstellen, dass ein Kanal offen ist. Die Natriumionen können jetzt in die Zelle strömen, was die Membran schnell depolarisiert – die Spannung wird positiver. Dieses schnelle Ansteigen der Spannung ist der sogenannte „Aufstrich“ des Aktionspotenzials. Kurz danach öffnen sich die Kaliumkanäle, allerdings etwas verzögert.
Kaliumionen strömen aus der Zelle heraus und tragen dazu bei, das Membranpotential wieder zu repolarisieren und letztlich sogar kurzzeitig hyperpolarisieren zu lassen, also negativer als das Ruhepotenzial zu werden. Gleichzeitig inaktivieren sich die Natriumkanäle wieder und schließen sich, was die Depolarisation stoppt. Die mathematische Beschreibung dieser Vorgänge erfolgt durch Differentialgleichungen, die sowohl die Spannung als auch den Zustand der Kanäle selbst (durch Variablen wie m, h für Natrium und n für Kalium) erfassen. Die Variablen stellen die Anteile der geöffneten Kanäle dar und sind wiederum abhängig von der Spannung. Dieses komplexe Wechselspiel macht die dynamische Entstehung eines Aktionspotentials möglich.
In virtuellen Neuronen ist das Zusammenspiel von Ionenkonzentrationen, Leitfähigkeiten und Spannungen so genau nachgebildet, dass es die realen elektrophysiologischen Phänomene sehr gut abbildet. Das Hodgkin-Huxley-Modell erlaubt es somit, die Auswirkung von Änderungen an bestimmten Parameterwerten zu testen. Beispielsweise kann untersucht werden, wie eine Veränderung der Leitfähigkeit von Natriumkanälen auf die Geschwindigkeit oder Höhe des Aktionspotentials wirkt. Das ist besonders wichtig, um pathologische Zustände zu simulieren, etwa im Kontext von neurologischen Erkrankungen wie Epilepsie, bei denen die Ionenkanalfunktion beeinträchtigt ist. Darüber hinaus bietet das Modell die Möglichkeit, externe Einflüsse wie Strominjektionen zu simulieren.
In Experimenten verwendeten Hodgkin und Huxley dafür Megaelektroden, die gezielt Strom in das Neuron einspeisten. Virtuelle Neuronen können diese Funktion nachempfinden, indem der Simulationscode erlaubt, zeitlich variable externe Ströme einzufügen. Dadurch können unterschiedliche Erregungszustände und Feuerraten von Neuronen getestet werden. Eine weitere wichtige Erkenntnis beim Aufbau des Modells ist die Volt- oder Spannungabhängigkeit der Kanäle. Die Leitfähigkeit der Natrium- und Kaliumkanäle hängt nämlich davon ab, wie hoch die momentane Membranspannung ist.
Das bedeutet, wenn die Spannung sich ändert, reagieren die Kanäle, indem sie sich schneller oder langsamer öffnen bzw. schließen. Die zugrundeliegende Biologie spiegelt sich in dieser Spannungssensitivität wider und ermöglicht die selbstverstärkende Dynamik der Aktionspotentialbildung. Die maximale Leitfähigkeit jedes Kanaltyps stellt eine obere Grenze dar. Ein Kanal kann höchstens vollständig geöffnet sein, was im Modell durch maximale Werte für m, n und h gekennzeichnet wird.
Die genaue Funktionsweise der Kanäle lässt sich auch als Wahrscheinlichkeiten interpretieren, dass einzelne Kanäle geöffnet oder geschlossen sind. Dabei ließ sich im Experiment beobachten, dass für Kaliumkanäle die Öffnung vom Zustand vier unabhängiger Untereinheiten abhängt, was sich mathematisch durch Potenzen ausdrücken lässt – ein Detail, das im Modell durch Potenzen von n (vierter Potenz) und m (dritter Potenz) integriert wurde. Ein weiteres biologisch relevantes Phänomen ist die Inaktivierung der Natriumkanäle, modelliert durch die Variable h. Sie beschreibt, wie sich Natriumkanäle nach Öffnung wieder inaktivieren und damit vorübergehend blockieren, bis sie sich reaktivieren. Dieses Teilen der Aktivierung (m) und Inaktivierung (h) war einer der großen Durchbrüche von Hodgkin und Huxley und erklärt, warum Aktionspotenziale nicht unendlich oft unmittelbar hintereinander abgefeuert werden können.
Neben Natrium und Kalium fügt das Modell noch einen sogenannten Leak-Kanal hinzu, der für andere Ionen und Leckströme steht. Dessen Leitfähigkeit bleibt dabei konstant und sorgt dafür, dass das Ruhepotenzial stabil bleibt und das System nicht in extremen Spannungen endet. Der gesamte Hodgkin-Huxley-Formalismus besteht somit aus einem Satz gekoppelter nichtlinearer Differentialgleichungen, die den zeitlichen Verlauf des Membranpotentials und der Kanalzustände beschreiben. Moderne Computer können diese Gleichungen numerisch lösen und damit das Verhalten eines virtuellen Neurons simulieren. Solche Simulationen erlauben eine Vielzahl von Untersuchungen.
Wie reagiert das Neuron auf unterschiedliche externe Stimuli? Wie verändern sich die Aktionspotenziale bei veränderter Kanalaktivität? Welche Effekte haben Mutationen in Ionenkanälen? Auch das Zusammenspiel mehrerer Neuronen, also neuronaler Netzwerke, kann so modellhaft erfasst werden, was für das Verständnis von Hirnfunktionen und neurologischen Störungen zentral ist. Das Verständnis und Beobachten der Variablen m, n und h liefert darüber hinaus Einblicke in die Biologie der Ionenkanäle selbst. Zum Beispiel öffnet sich der Natriumkanal (m) sehr schnell bei Depolarisation, während die Inaktivierung (h) zeitverzögert reagiert. Die Kaliumkanäle (n) öffnen langsamer, was den Rückgang des Aktionspotentials steuert. Das Zusammenspiel sorgt dafür, dass das Aktionspotential charakteristische Phasen von Aufstrich, Abfall und Nachhyperpolarisation durchläuft.
Neben den rein biophysikalischen Grundlagen erleichtert das Hodgkin-Huxley-Modell auch das Verständnis pathologischer Situationen. So kann simuliert werden, wie eine Vergiftung durch Tetrodotoxin, das Natriumkanäle blockiert, sich auf die Aktionspotentialbildung auswirkt. Ebenso können die Effekte genetischer Veränderungen, die zu veränderten Kanalleitfähigkeiten führen, mathematisch erfasst und besser verstanden werden. Die Implementierung eines virtuellen Neurons nach Hodgkin und Huxley auf einem Computer lässt sich zudem modular erweitern. Zahlreiche Programmierumgebungen und Bibliotheken bieten Werkzeuge, um die komplexen Gleichungen effizient zu lösen.
Ein solches virtuelles Neuron dient dann sowohl als Forschungsinstrument in der Neurowissenschaft als auch als Grundlage für Anwendungen in der Robotik oder im Bereich künstliche Intelligenz. Am Ende entsteht durch diese Kombination aus experimenteller Forschung, biologischem Verständnis und mathematischer Modellierung ein mächtiges Instrument, mit dem die Funktionsweise von Nervenzellen besser durchdrungen werden kann. Das Hodgkin-Huxley-Modell ist dabei ein Meilenstein, der den Weg zur modernen neuronalen Simulation geebnet hat. Seine Prinzipien bilden die Basis für komplexere Modelle, die weitere Ionenarten, Kanaltypen oder auch synaptische Vorgänge integrieren und so Schritt für Schritt das Zusammenspiel neuronaler Prozesse nachvollziehbar machen. Die Entwicklung virtueller Neuronen trägt nicht nur zur Grundlagenforschung bei, sondern bietet auch Impulse für die Medizin.
So können virtuelle Modelle genutzt werden, um Medikamentenwirkungen zu testen oder neuartige Therapieansätze bei neuronalen Erkrankungen zu entwickeln. Die enge Verzahnung von Biologie, Mathematik und Informatik macht das Gebiet besonders dynamisch und zukunftsträchtig. Insgesamt zeigt die Nachbildung von virtuellen Neuronen anhand des Hodgkin-Huxley-Modells eindrucksvoll, wie komplexe biologische Systeme auf mathematische Modelle reduziert und so simuliert werden können. Dies trägt erheblich zur Erweiterung unseres Verständnisses von neuronalen Vorgängen bei und eröffnet spannende Perspektiven für Forschung und Praxis.