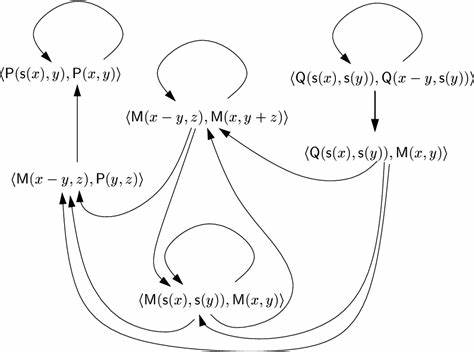
Die Welt der abstrakten Algebra und formalen Sprachen ist reich an komplexen Strukturen und Lösungsansätzen, die durch innovative Algorithmen beherrschbar werden. Einer der bedeutendsten Algorithmen in diesem Zusammenhang ist der Knuth-Bendix Algorithmus, der speziell für das Problem der Vereinfachung von Wörtern in endlichen Präsentationen von Monoiden und Gruppen entwickelt wurde. Der Knuth-Bendix Completion Calculator stellt dabei ein kraftvolles Werkzeug dar, das diese theoretischen Konzepte zugänglich macht und deren praktische Anwendung erheblich erleichtert. Monoide und Gruppen sind fundamentale algebraische Strukturen, die durch ein stringentes Regelwerk definiert werden. In vielen Fällen sind diese Strukturen durch eine endliche Menge von Erzeugern und Relationen beschrieben.
Die Relationen wiederum sind als Gleichungen zwischen sogenannten Wörtern formuliert – das heißt, Sequenzen von Symbolen, welche die Erzeuger repräsentieren. Das Ziel besteht darin, eine Menge von Rewrite-Regeln zu erzeugen, die erlaubt, jedes Wort in eine eindeutige, minimalste Form zu überführen. Diese Normalformen erleichtern nicht nur die Gleichheitsprüfung, sondern bilden auch die Grundlage für weiterführende algebraische Untersuchungen und Anwendungen. Der Knuth-Bendix Algorithmus ist ein entscheidendes Verfahren zur Erreichung dieser Zielsetzung. Gegeben eine Menge von Gleichungen über Wörter, verarbeitet der Algorithmus diese, um eine konvergente Menge von Umformungsregeln zu generieren.
Durch wiederholte Anwendung dieser Regeln auf Teilwörter kann jedes Wort zu seiner kleinsten äquivalenten Form reduziert werden. Das Verfahren stellt sicher, dass jede Reduktion deterministisch ist und keine zwei unterschiedlichen Endformen für äquivalente Wörter existieren, was die Konsistenz garantiert. Der Knuth-Bendix Completion Calculator implementiert diesen Algorithmus präzise und benutzerfreundlich. Anwender geben eine Reihe von Wortgleichungen ein, welche die Relationen der algebraischen Struktur beschreiben. Dabei können komplexe Ausdrücke mit Wiederholungen durch die Notation (.
.. )^n flexibel formuliert werden. Der Rechner verarbeitet diese Eingaben, erzeugt die Rewrite-Regeln und ermöglicht die Reduktion beliebiger weiterer Wörter nach denselben Regeln. Dadurch lässt sich überprüfen, ob zwei Wörter äquivalent sind, da sie auf dieselbe Normalform reduziert werden müssten.
Ein herausragendes Merkmal dieses Tools ist die Transparenz während des Verarbeitungsprozesses. Die Nutzer können die einzelnen Schritte verfolgen, wie aus den gegebenen Gleichungen neue, potenziell noch fehlende Regeln abgeleitet werden. Dies unterstützt das Verständnis des Algorithmus und gewährt Einblick in die zugrunde liegende algebraische Struktur. Zudem zeigt der Rechner, wie durch sukzessive Verarbeitung und Konfliktauflösung eine konsistente Menge von Regeln entsteht, die den ursprünglichen Gleichungen äquivalent bleibt. Die praktische Bedeutung des Knuth-Bendix Completion Calculators liegt in vielfältigen Bereichen der Mathematik und Informatik.
In der automatischen Theorembeweisung wird er genutzt, um komplexe Gleichungssysteme systematisch zu vereinfachen, sodass Aussagen leichter überprüfbar sind. In der Theorie der formalen Sprachen sowie in der Programmverifikation helfen die erarbeiteten Normalformen, komplexe Aussagen über Programmeigenschaften oder sprachliche Transformationsregeln handhabbar zu machen. Insbesondere in der Computeralgebra ist die Möglichkeit, Endungen und Umformungen automatisch zu berechnen, ein großer Fortschritt. Komplexe algebraische Berechnungen, die von Hand oder durch einfache Werkzeuge kaum vollständig durchführbar sind, lassen sich so effizient realisieren. Die Reduktion auf eindeutige Normalformen ist auch essenziell für die Isomorphieprüfung von algebraschen Objekten, wo die Identifikation gleicher Strukturen trotz unterschiedlicher Darstellungen notwendig ist.
Interessant sind auch die mathematischen Voraussetzungen und Herausforderungen, die der Knuth-Bendix Algorithmus behandelt. Während er für viele Präsentationen konvergente Regeln erzeugt, gibt es auch Fälle, in denen keine vollständige konvergente Regelmenge existiert. In solchen Situationen kann der Completion Calculator zumindest die bisher ableitbaren Regeln anonym erzeugen, was Forscher bei der weiteren Analyse unterstützt. Die Fähigkeit, mit potentiell nicht abschließbaren Systemen zu arbeiten, macht das Tool besonders flexibel. Darüber hinaus bieten moderne Varianten und Erweiterungen des Knuth-Bendix Algorithmus weiterführende Möglichkeiten.
So lassen sich beispielsweise gewichtete oder orderbasierte Umformungen nutzen, um die Effizienz der Reduktionen zu verbessern oder spezifische Prioritäten zu setzen. Der Knuth-Bendix Completion Calculator bildet eine solide Basis, die solche Erweiterungen ermöglicht und deren Integration in Arbeitsabläufe erleichtert. Für Anwender ohne tiefgehende Kenntnisse in theoretischer Algebra bietet der Rechner eine intuitive Schnittstelle und klare Rückmeldungen. Diese Benutzerfreundlichkeit fördert den Zugang zu komplexen mathematischen Konzepten und erleichtert die Integration in Lern- und Forschungsumgebungen. Die Möglichkeit, eigene Gleichungssysteme flexibel einzugeben und die Auswirkungen der Regelableitung unmittelbar zu sehen, macht das Tool zu einem wertvollen Begleiter für Studierende, Lehrende und Forschende gleichermaßen.
Insgesamt betrachtet ist der Knuth-Bendix Completion Calculator ein elementares Instrument für jeden, der sich mit der Vereinfachung von algebraischen Wortgleichungen beschäftigt. Die Kombination aus algorithmischer Präzision, anwenderorientierter Gestaltung und fachlicher Tiefe sichert dem Tool eine wichtige Rolle in modernen mathematischen und informatischen Anwendungen. Durch die Ermöglichung effizienter Normalformberechnungen trägt es wesentlich zur Lösung komplexer Aufgaben in der algebraischen Strukturanalyse bei. Die Nutzung eines solchen Rechners ist auch ein Schritt in Richtung automatisierte Mathematik, wo Algorithmen selbstständig Strukturen erkennen, vereinfachen und klassifizieren können. So entsteht eine zunehmend leistungsfähige Unterstützung für theoretische und praktische Problemstellungen, die zuvor nur mit großer Mühe oder gar nicht gelöst werden konnten.
Der Knuth-Bendix Completion Calculator steht damit für Fortschritt sowohl in der Theorie als auch in der Anwendung und bietet eine Brücke zwischen abstrakter Mathematik und konkreter Umsetzung. Zusammenfassend bietet der Knuth-Bendix Completion Calculator eine einzigartige Möglichkeit, komplexe Wortgleichungssysteme zu strukturieren und zu vereinfachen. Es handelt sich um ein unerlässliches Werkzeug in der automatischen Vereinfachung von endlichen Präsentationen algebraischer Strukturen, das mit seiner klaren Ergebnisdarstellung und umfassenden Regelgenerierung überzeugt. Optimal einsetzbar in Forschung, Lehre und Praxis, stellt es einen bedeutenden Meilenstein in der computergestützten Algebra dar.