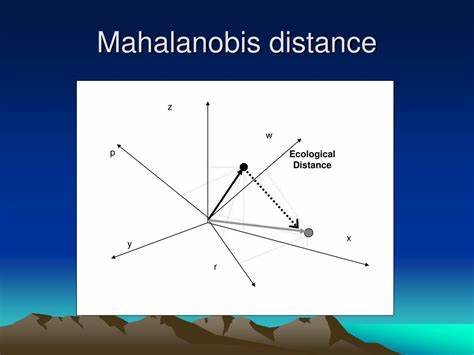
Die Mahalanobis-Distanz ist ein grundlegendes Konzept in der Statistik und multivariaten Datenanalyse, das erstmals 1936 von dem indischen Statistiker P. C. Mahalanobis eingeführt wurde. Sie bietet eine Möglichkeit, die Entfernung eines Punktes von einer Verteilung zu messen, wobei nicht nur die Lage des Punktes, sondern auch die Form und Streuung der Verteilung berücksichtigt werden. Dieser Ansatz hebt sich deutlich von klassischen euklidischen Entfernungen ab, indem er Kovarianzen und Korrelationen der Daten mit einbezieht und so eine deutlich aussagekräftigere Distanzmetrik in mehrdimensionalen Räumen schafft.
Die Mahalanobis-Distanz wird in vielen Bereichen wie der Mustererkennung, Klassifikation, Anomalieerkennung und sogar in der Finanzanalyse verwendet. Die Grundlagen der Mahalanobis-Distanz basieren auf der Annahme, dass die Daten eine Mittelwertverteilung besitzen, deren Lage durch den Mittelwertvektor bestimmt ist. Zusätzlich spielt die Kovarianzmatrix eine entscheidende Rolle, da sie die Varianzen und Korrelationen der verschiedenen Merkmale in den Daten repräsentiert. Während eine einfache Distanzmessung wie die euklidische Distanz nur den Abstand in einem geometrischen Sinne misst, skaliert die Mahalanobis-Distanz die Differenz zwischen einem Datenpunkt und dem Mittelwert anhand der Form der Verteilung. Dadurch erhält man eine dimensionslose Distanz, die sinnvolle Vergleiche über verschiedene Dimensionen und Einheiten hinweg ermöglicht.
Mathematisch wird die Mahalanobis-Distanz eines Punktes x von einer multivariaten Verteilung mit Mittelwert μ und Kovarianzmatrix Σ durch den Ausdruck (x−μ)ᵀΣ⁻¹(x−μ) definiert. Dabei ist Σ⁻¹ die Inverse der Kovarianzmatrix, was unterstreicht, dass die Beziehungen zwischen den einzelnen Variablen berücksichtigt werden. Wenn die Kovarianzmatrix die Identitätsmatrix wäre, würde sich die Mahalanobis-Distanz zur euklidischen Distanz vereinfachen. In der Praxis bedeutet das, dass die Distanz entlang von Achsen mit hoher Varianz weniger stark gewichtet wird, während Abweichungen in Richtungen mit geringer Varianz stärker ins Gewicht fallen. Ein weiterer wichtiger Aspekt der Mahalanobis-Distanz ist ihre Beziehung zur multivariaten Normalverteilung.
Für solche Verteilungen entspricht die Kontur konstanter Mahalanobis-Distanz einer Ellipse (in höheren Dimensionen einem Ellipsoid), die die Form und Streuung der Daten widerspiegelt. Die Quadrate der Mahalanobis-Distanzen folgen einer Chi-Quadrat-Verteilung, was statistische Tests ermöglicht, um beispielsweise Ausreißer zu erkennen oder die Zugehörigkeit eines Punktes zu prüfen. Auf diese Weise können Forscher und Analysten objektivere Aussagen über die Wahrscheinlichkeit treffen, dass ein neuer Datenpunkt zu einer bestimmten Population gehört. Die Anwendungsmöglichkeiten der Mahalanobis-Distanz sind vielseitig. In der Mustererkennung und Klassifikation wird sie verwendet, um Testdaten bestimmten Klassen zuzuordnen, indem die Distanz zu den Mittelwerten der Klassen berechnet wird.
Ein Beispiel dafür ist die lineare Diskriminanzanalyse, bei der die Mahalanobis-Distanz maßgeblich zur Trennung von Klassen beiträgt. Auch in der Ausreißererkennung ist sie sehr effektiv, da ungewöhnliche Datenpunkte in Bezug auf die multivariate Verteilung oft durch eine große Mahalanobis-Distanz identifiziert werden können. Anders als beim individuellen Vergleich der Variablen berücksichtigt die Mahalanobis-Distanz zudem die Gesamtstruktur der Daten. Ein praktisches Beispiel ist die Ökologie, wo die Mahalanobis-Distanz verwendet wird, um ökologische Nischen zu modellieren. Da ökologische Daten oft multivariat und stark korreliert sind, ist die einfache euklidische Distanz unzureichend.
Die Mahalanobis-Distanz kann die fundamental-ökologische Nische in einem Datenraum abbilden und entsprechende Habitatzonen identifizieren. Ebenso wird sie in der Finanzwelt zum Beispiel im Rahmen der Risikoanalyse eingesetzt, um ungewöhnliche Marktbewegungen zu erkennen und Indexe für Turbulenzen zu erstellen. Trotz ihrer zahlreichen Vorteile gibt es auch einige Herausforderungen bei der Anwendung der Mahalanobis-Distanz. Die Berechnung der Kovarianzmatrix und deren Inverse kann bei großen Dimensionalitäten und kleinen Stichproben problematisch sein, da die Matrix dann nicht invertierbar oder schlecht konditioniert sein kann. Um dem entgegenzuwirken, nutzen Experten robuste Ansätze zur Schätzung von Lage und Streuung, etwa den Minimum Covariance Determinant oder den Minimum Volume Ellipsoid, die weniger empfindlich gegenüber Ausreißern sind.
Zudem wird häufig eine Vorverarbeitung angewandt, bei der die Datendimensionen reduziert oder durch Dimensionsreduktionstechniken wie der Hauptkomponentenanalyse transformiert werden. Technisch gesehen können Programmierer und Datenanalysten die Mahalanobis-Distanz in verschiedensten Programmiersprachen unkompliziert berechnen. Bibliotheken in R, Python (SciPy), MATLAB oder Julia bieten Funktionen an, die auf Benutzerfreundlichkeit ausgelegt sind. Dies erleichtert die Integration der Distanz in Analyse-Pipelines und unterstützt die Entwicklung von Klassifikatoren oder Ausreißererkennungsalgorithmen. Zusammenfassend lässt sich sagen, dass die Mahalanobis-Distanz eine bedeutende Rolle in der modernen Statistik und Datenanalyse spielt.
Durch die Einbeziehung der Kovarianzstruktur schafft sie eine distanzbasierte Metrik, die die komplexe Struktur multivariater Daten angemessen widerspiegelt. Ob in den Naturwissenschaften, der Finanzwirtschaft oder im maschinellen Lernen – die Mahalanobis-Distanz ermöglicht präzise Klassifikationen, robuste Ausreißererkennungen und ein fundiertes Verständnis von Datenverteilungen. Wer sich eingehend mit multivariaten Analysen beschäftigt, sollte die Mahalanobis-Distanz als essenzielles Werkzeug betrachten und ihre theoretischen und praktischen Eigenschaften sorgfältig nutzen.