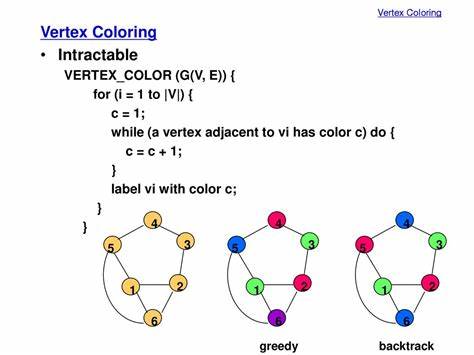
Die Graph-Vertex-3-Färbung, oft einfach als 3-Färbung bezeichnet, gehört zu den Kernproblemen der theoretischen Informatik und der Kombinatorik. Dieses Problem beschäftigt sich mit der Frage, ob es möglich ist, die Knoten eines gegebenen Graphen mit genau drei Farben so einzufärben, dass keine zwei benachbarten Knoten die gleiche Farbe besitzen. Trotz seiner scheinbar einfachen Formulierung hat das Problem tiefgreifende Konsequenzen für unser Verständnis von Berechenbarkeit, Komplexität und informatischer Optimierung. Die Frage, ob eine informelle, also leicht verständliche und dennoch nachvollziehbare Beweisführung für die NP-Vollständigkeit dieses Problems besteht, stößt daher auf Interesse innerhalb der Fachwelt und darüber hinaus. Die NP-Vollständigkeit (NPC) ist ein Konzept der theoretischen Informatik, das einen besonders schwierigen Komplexitätsgrad innerhalb der Klasse der NP-Probleme beschreibt.
NP steht für die Menge der Entscheidungsprobleme, deren Lösungen sich in polynomialer Zeit verifizieren lassen, obwohl eine effiziente Methode zur Findung der Lösung selbst unbekannt ist. Ein Problem wird dann NP-vollständig genannt, wenn es selbst in NP liegt und zugleich jedes andere Problem in NP auf es in polynomieller Zeit reduzieren lässt. Die 3-Färbung gehört zu jenen klassischen Problemen, die dazu dienten, die Grenzen der effizienten Berechenbarkeit zu definieren. Historisch betrachtet ist die erste offizielle Identifikation der NP-Vollständigkeit der Graph-Vertex-3-Färbung auf die Arbeiten von Richard Karp zurückzuführen. Im Jahr 1972 veröffentlichte Karp einen bahnbrechenden Artikel, in dem er 21 fundamentale NP-vollständige Probleme auflistete, unter ihnen das Problem der Graphfärbung mit drei Farben.
Dieser Beweis ist formal, mathematisch präzise und gilt bis heute als maßgeblich. Allerdings ist diese Art von Beweis für Einsteiger und selbst für viele Praktiker oftmals schwer zu durchdringen, da sie eine tiefgehende Kenntnis der Komplexitätstheorie und der Reduktionstechniken voraussetzt. Das Interesse an einer informellen Beweisführung rührt daher, dass viele Menschen aus Fachgebieten wie Softwareentwicklung, angewandter Mathematik oder Informatikdidaktik zwar das Problem und seine Bedeutung verstehen, aber Schwierigkeiten haben, die formale Herleitung nachzuvollziehen. Eine verständliche Darstellung könnte die Hürde senken und damit das Wissen um die fundamentalen Grenzen algorithmischer Lösbarkeit erweitern. Dadurch ließe sich der Zugang zu einem zentralen Thema der theoretischen Informatik erleichtern und ein breiteres Publikum könnte sich informieren und weiterbilden.
Der Grundgedanke hinter einer informellen Beweisführung besteht darin, auf komplizierte Formalismen zu verzichten, stattdessen durch anschauliche Analogien, konkrete Beispiele und intuitive Erklärungen die Kernidee des Beweises zu vermitteln. Konkret bedeutet das im Fall der Graph-Vertex-3-Färbung, den Weg zu zeigen, wie man aus einem bekannten NP-vollständigen Problem – zum Beispiel aus dem Satisfiability-Problem (SAT) – das Färbungsproblem effizient transformieren kann, sodass deren Lösungen äquivalent sind. Solch eine Transformation nennt man Reduktion und sie ist der Schlüsselmechanismus in der Komplexitätstheorie. Die Schwierigkeit besteht darin, eine solche Reduktion leicht verständlich zu präsentieren, ohne dabei an Genauigkeit zu verlieren. Es gilt zu zeigen, dass jedes Beispiel einer erfüllbaren Formel in eine Graphstruktur übersetzt werden kann, in der die 3-Färbung genau dann möglich ist, wenn die Formel erfüllbar ist.
Diese Eins-zu-eins-Beziehung bildet das Herzstück der NP-vollständigkeitsbewertung. In der Praxis bedeutet das: Es gibt eine Methode, um logische Formeln in Graphen umzuwandeln, sodass das Finden einer passenden 3-Färbung direkt mit einer Lösung der ursprünglichen Formel korrespondiert. Auf diese Weise kann geklärt werden, dass die Schwierigkeit beim Lösen von SAT um keinen Deut geringer ist als beim Lösen der 3-Färbung, womit die NP-Vollständigkeit bestätigt wird. Die informelle Beweisführung würde genau diese Konstruktion erklären, mit einfachen Metaphern und Schritt-für-Schritt-Beispielen. Die Relevanz dieser Beweisführung geht über reines akademisches Interesse hinaus.
Viele Probleme in der Praxis, beispielsweise in der Ressourcenallokation, der Zeitplanung oder der Netzwerkanalyse, lassen sich auf Varianten der Graphfärbung zurückführen. Das Verständnis ihrer inhärenten Schwierigkeit hilft dabei, realistische Erwartungen an algorithmische Lösungen zu formulieren und Effizienzgrenzen besser abzuschätzen. Gerade in Zeiten wachsender Datenmengen und komplexer Systeme gewinnt eine solche Klarheit an Bedeutung. In der Community der theoretischen Informatik und darüber hinaus wurde das Thema bereits angeregt diskutiert. Ein Vertreter dieser Diskussion ist Colin Wright, der in einer öffentlichen Diskussionsplattform darauf hinwies, dass es Interesse an einem informellen Beweis gäbe und zugleich feststellte, dass diese Nachfrage eher gering ausfiel.
Das zeigt eine gewisse Zurückhaltung, möglicherweise auch eine gewisse Sorgfalt, die mit der Erstellung eines solchen Beweises verbunden ist, oder schlicht die Herausforderung, komplexe theoretische Inhalte auch informell korrekt und nachvollziehbar zu vermitteln. Trotz dieser Vorbehalte wäre die Verbreitung eines gut aufbereiteten, informellen Beweises zur NP-Vollständigkeit der Graph-Vertex-3-Färbung eine Bereicherung für die Fachwelt und die breitere Öffentlichkeit. Insbesondere Studierende könnten so leichter einen Zugang zu einem einschlägigen, aber komplexen Thema bekommen. Zudem könnten Entwickler und Forscher Inspiration erhalten, um alternative Lösungsansätze und Heuristiken für schwierige graphbasierte Probleme zu entwickeln. Zusammenfassend ist die Graph-Vertex-3-Färbung ein Paradebeispiel für die Grenzen des algorithmisch Machbaren.
Ihre NP-Vollständigkeit ist ein Eckpfeiler der Komplexitätstheorie, dessen offizielle Formulierung als Karp’sches Reduktionsproblem etabliert ist. Eine informelle Beweisführung stellt eine innovative Möglichkeit dar, dieses komplexe Konzept zugänglicher zu machen und einem breiteren Kreis verständlich zu vermitteln. Die Herausforderung dabei ist, die Präzision nicht zu opfern und dennoch die Hürde der Formalismen zu vermeiden. Das Thema hat deshalb sowohl didaktischen als auch wissenschaftlichen Wert und verdient weitere Aufmerksamkeit und Unterstützung.