Die moderne Welt ist untrennbar mit Computern verbunden. Doch was genau macht ein physikalisches System zum Computer? Diese Frage ist gar nicht so trivial, wie sie scheint. Während eine klassische Digitalklappe offensichtlich ein Computer ist, wird es schwieriger, die Rechenfähigkeit von nicht-standardisierten oder biologischen Systemen zu bestimmen. Ab wann können Prozesse in der Natur wirklich als Rechnung gelten? Und was unterscheidet bloß eine physikalische Entwicklung von einer echten Berechnung? Die Herausforderung beginnt mit der Unterscheidung zwischen abstrakten Berechnungen und deren Umsetzung in der physischen Welt. Computation an sich ist ein mathematisches und logisches Konzept, das unabhängig von Realisierung existiert.
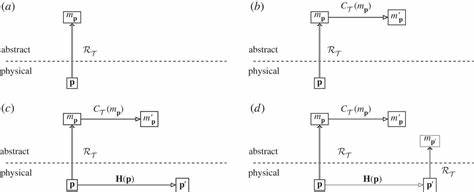
Ein Algorithmus ist eine formale Abfolge von Regeln und Operationen, abstrakt definiert und ungebunden an jegliche konkrete Maschine. Im Gegenteil dazu steht der Computer als physisches Objekt: ein System aus Elektronen, Atomen und physikalischen Prozessen, das real existiert und natürliche Gesetze befolgt. Zentral für das Verständnis, wann ein physikalisches System wirklich rechnet, ist die sogenannte Repräsentationsrelation. Physik arbeitet traditionell mit Modellen – abstrakten Beschreibungen der realen Welt. Ein Elektron wird durch eine Wellenfunktion dargestellt, Planetenbahnen durch Differentialgleichungen.
Diese Modellierung übersetzt die komplexe Realität in mathematische Objekte, mit denen man vorhersagen, simulieren und reflektieren kann. Eine wichtige Erkenntnis dabei ist, dass diese Repräsentationsrelation asymmetrisch ist. Wir können physikalische Systeme abstrakt modellieren, doch das Umgekehrte – das Instanziieren eines abstrakten Modells in einer physischen Realität – ist deutlich schwieriger und nicht immer möglich. Dies betrifft direkt auch das Computingsystem: Nicht jedes abstrakte Rechenmodell lässt sich beliebig in physikalische Strukturen übersetzen, die am Ende auch zuverlässig die erwünschte Rechnung durchführen. Physikalische Theorien ermöglichen es, dieses „Umkehren“ unter besonderen Bedingungen durchzuführen.
Wenn eine Theorie ausreichend präzise und geprüft ist, kann sie nicht nur erklären, wie ein gegebenes System funktioniert, sondern auch vorhersagen, wie ein neu zu bauendes System zu seinem abstrakten Modell instanziiert werden kann. Technologie und Ingenieurwesen sind damit Praktiken des „Rückwärtsmodellierens“: Sie beginnen mit einer abstrakten Spezifikation und konstruieren daraus ein konkretes physisches System, das diese erfüllt. Erst unter dieser Voraussetzung kann von einem Rechner im physikalischen Sinn gesprochen werden. Dabei spielt der Begriff des „Berechnens“ eine ganz entscheidende Rolle. Es reicht nicht, dass ein physikalisches System einfach nur irgendeine physikalische Entwicklung durchläuft.
Damit gerechnet wird, muss das System in der Lage sein, eine abstrakte Berechnung abzubilden – also Daten auf eine konkrete Weise zu kodieren, diese physikalisch zu manipulieren und anschließend wieder sinnvoll zu dekodieren, sodass das Resultat der physischen Evolution einem vorab definierten abstrakten Rechenprozess entspricht. Um diese Kodierung und Dekodierungressource nachvollziehbar zu machen, ist die Präsenz eines sogenannten „computational entity“ bzw. „Recheneinheit“ notwendig. Dabei handelt es sich um ein Objekt oder eine Entität, die die abstrakte Interpretation in einer physischen Umgebung realisiert. Diese Entität muss nicht menschlich oder gar bewusst sein; sie ist vielmehr die Voraussetzung dafür, dass ein physikalisches System als Computer fungieren kann, indem sie die für die Berechnung notwendige Repräsentationsrelation etabliert.
Dieser Aspekt verhindert auch den populären Fehlschluss, dass „alles im Universum eine Berechnung“ sei. Würde jede physikalische Bewegung als Berechnung gelten, böte dies zwar eine metaphysische Sichtweise, doch praktisch wäre sie wertlos, da dadurch der Begriff verwaschen und jegliche Unterscheidung verlorenging. Erst die Anforderung, dass eine Entität den Repräsentationsprozess durchführt und eine stabile Theorie hinter der Zuordnung steht, differenziert echte Rechnungen von physikalischem Rauschen. Weiterhin muss ein physikalisches System über zumindest eine fundamentale dynamische Operation verfügen, durch die Eingabedaten verarbeitet und Ausgangsdaten erzeugt werden können. Dies sind etwa logische Gatter bei digitalen Computern.
Die Integration dieser Operationen sowie deren Zusammensetzung müssen so gestaltet sein, dass theoretisch und experimentally die Repräsentationsdiagramme „kommutieren“ – dass bedeutet, physikalische Prozesse und ihre abstrakten Beschreibungen führen zum gleichen Ergebnis. Die Idee der stetigen Kommutativität von Diagrammen stammt aus der Philosophie der Wissenschaft und beschreibt das Vertrauen in Theorien: Die Abbildung von Realität zu Modell, die Auflösung von Zustandsübergängen im Modell und die Vergleichbarkeit von physischem und abstraktem Ergebnis müssen konsistent sein. Nur wenn diese Bedingung erfüllt ist, kann man mit ausreichender Sicherheit sagen, dass das physikalische System die gewünschte Berechnung ausführt. Dies hat weitreichende Folgen für neuartige und unkonventionelle Rechenmodelle wie biologische Systeme, Quantencomputer oder physikalische Systeme wie Seifenfilme oder sogar Faltungsvorgänge in Proteinen. Ohne eine ausgereifte Theorie für die physikalischen Komponenten und deren Zusammenspiel kann man nicht zuverlässig sagen, dass diese Systeme tatsächlich Rechnungen durchführen.
Stattdessen sind experimentelle Untersuchungen oft eher Versuche, das System besser zu verstehen und eine physikalische Theorie aufzubauen, als dass tatsächlich Berechnungen durchgeführt würden. Simulation stellt einen Sonderfall dar, bei dem ein physikalisches System dazu benutzt wird, das Verhalten eines anderen physikalischen Systems vorherzusagen. Auch hier ist es essentiell, dass Abbildung und Kodierung des simulierten Systems in den Simulationsapparat durch klare Repräsentationsrelationen erfolgt. Simulation ist damit ein komplexes Zusammenspiel von Abbildungen verschiedener Abstraktionsebenen. Zusammenfassend lässt sich sagen, dass ein physikalisches System genau dann als Computer bezeichnet werden kann, wenn es nicht nur in seinem Zustand einer Berechnung entspricht, sondern diese Berechnung auch bewusst encodiert und decodiert wird, auf einer gut geprüften physikalischen Theorie basiert, die Evolution der Zustände eine definierte dynamische Operation ist und die gesamten Repräsentationsdiagramme kommutieren.
Die Präsenz eines computational entity garantiert, dass die physikalischen Prozesse nicht nur zufällige Ereignisse sind, sondern gezielt zur Berechnung eingesetzt werden. Die Herausforderung für die Zukunft besteht darin, diese Bedingungen weiter zu erforschen und zu implementieren, insbesondere bei unkonventionellen Rechenansätzen. Nur so können wir weiterhin sicher sein, wann ein physikalisches System tatsächlich rechnet – und wann wir lediglich das physikalische Verhalten beobachten, ohne davon zu profitieren. Dieses Verständnis ermöglicht darüber hinaus eine greifbare Verbindung zwischen abstrakten mathematischen Konzepten und der physikalischen Wirklichkeit, setzt den Rahmen für technologische Innovation und sorgt für Klarheit in der Debatte um das Wesen von Information, Computation und der Rolle physikalischer Systeme in der Informationsverarbeitung.