Die Bewertung von Finanzderivaten stellt eine der zentralen Herausforderungen im Bereich des modernen Finanzwesens dar. Insbesondere Optionen, als eine der bedeutendsten Derivatearten, eröffnen Anlegern vielfältige Möglichkeiten zur Absicherung und Spekulation. Die präzise und effiziente Preisfindung solcher Optionen ist jedoch komplex und erfordert fundierte mathematische und informatische Ansätze. Mit der Programmiersprache C++ bietet sich eine leistungsstarke Plattform, um Modelle für die Optionsbewertung zu implementieren und dabei sowohl klassische als auch moderne Verfahren zu nutzen. Im Kern beschäftigt sich das Thema mit der Berechnung von Optionspreisen sowie der Bestimmung sogenannter „Greeks“.
Diese Sensitivitätskennzahlen helfen Investoren, das Risiko und die Reaktion des Optionswerts auf Veränderungen verschiedener Parameter wie Kurs, Volatilität, Zeit oder Zinssätze zu verstehen und zu steuern. Die genaue Modellierung dieser Größen ist besonders wichtig, um fundierte Handelsentscheidungen treffen und Portfolios effektiv managen zu können. Das vorgestellte C++-Projekt bietet eine umfassende Implementierung verschiedener Optionsarten: europäische, amerikanische und asiatische Optionen. Jede dieser Optionstypen besitzt charakteristische Eigenschaften hinsichtlich Ausübungszeitpunkten und Berechnungsmethoden. Europäische Optionen können nur am Ende der Laufzeit ausgeübt werden, was eine relativ einfache Modellierung erlaubt.
Amerikanische Optionen hingegen erlauben die Ausübung jederzeit innerhalb der Laufzeit, was die mathematische Behandlung komplexer macht. Asiatische Optionen zeichnen sich durch eine Abhängigkeit vom Durchschnittspreis einer zugrundeliegenden Aktie oder eines Indikators während der Laufzeit aus, was wiederum andere Berechnungsmethoden erfordert. Für europäische Optionen wird primär auf das Black-Scholes-Merton-Modell zurückgegriffen. Dieses gilt als klassisches Verfahren zur Optionspreisbestimmung und basiert auf der Annahme einer lognormalverteilten Kursentwicklung sowie konstanten Volatilität. Die Implementierung im C++-Code umfasst sowohl die analytische Berechnung der Optionspreise als auch die Monte-Carlo-Simulation, welche als numerische Methode auch bei komplexeren Marktsituationen angewandt wird.
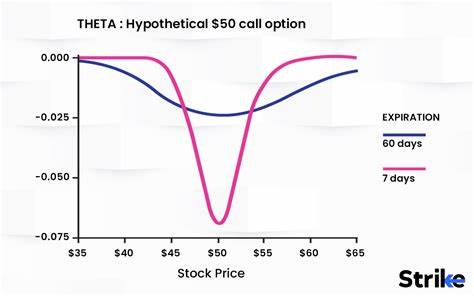
Mit Hilfe der Monte-Carlo-Simulation können Zustände der zugrundeliegenden Variablen entlang vieler Pfade simuliert und daraus Durchschnittswerte für den Optionspreis berechnet werden. Ein besonders wertvoller Aspekt dieser Implementierung ist die Berechnung der Greeks. Während das Black-Scholes-Modell analytische Formeln für Delta, Gamma, Theta, Vega und Rho bietet, nutzt das Projekt darüber hinaus finite Differenzenmethoden, um diese Sensitivitäten auch für nicht-analytisch lösbare Optionen, wie z.B. amerikanische oder asiatische Optionen, zu bestimmen.
Die Verwendung von finite Differenzen eröffnet die Möglichkeit, kleine Veränderungen der Eingabeparamater gezielt zu untersuchen und daraus die Ableitungen beziehungsweise Sensitivitäten abzuleiten. Für asiatische Optionen kommt vor allem die Monte-Carlo-Simulation zum Einsatz. Aufgrund der komplexen Abhängigkeit vom Durchschnittskurs ist eine analytische Lösung kaum möglich. Die Simulation basiert auf der Generierung realitätsnaher Spotpreis-Pfade, welche mittels geometrischer Brownscher Bewegung modelliert werden. Die darauf basierende Preiskalkulation berücksichtigt den Durchschnitt aller simulierten Pfade und ermöglicht so eine realistische Bewertung der asiatischen Optionen.
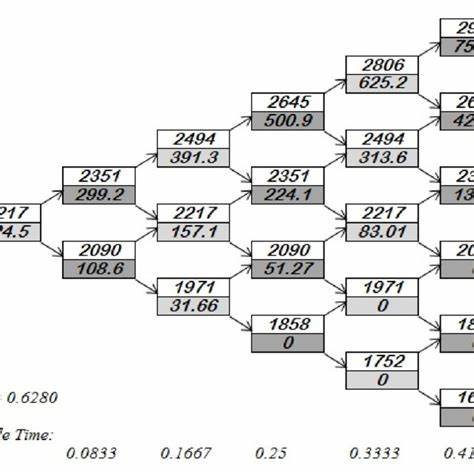
Auch hier berechnet das Programm die Sensitivitäten über finite Differenzen, um die Wahrscheinlichkeit von Preisschwankungen durch Markteinflüsse besser abschätzen zu können. Die Bewertung amerikanischer Optionen erfolgt über ein Binomialbaum-Modell. Dieses diskrete Zeitmodell simuliert mögliche Kursentwicklungen in einzelnen Schritten und erlaubt die Berücksichtigung der frühzeitigen Ausübungsmöglichkeit. Der sogenannte Backward-Induktionsprozess durchläuft das Baumgerüst vom Ende der Laufzeit zurück zum aktuellen Zeitpunkt und bestimmt mit Hilfe der auftretenden Cashflows den Optionswert in jedem Zustand. Diese Methode bietet eine praktikable Möglichkeit, die American-Optionen akkurat abzubilden und deren Preise zu bestimmen.
Darüber hinaus unterstützt das Projekt die Analyse der Amerikanischen Optionen hinsichtlich der Greeks. Da es für diese Optionstypen keine geschlossene analytische Form gibt, berechnet das Programm mittels finite Differenzierung die Sensitivitätskennzahlen, indem es kleine Veränderungen in den Eingabeparametern vornimmt und deren Auswirkungen auf den Preis misst. Dies ist essentiell, um die Reaktion der Option auf Marktbewegungen bewerten zu können. Technisch gesehen besteht das Projekt aus verschiedenen Quellcodedateien, die die zentrale Funktionalität modular abbilden. Beispielsweise kontrolliert NormRand_Gen.
cpp die Erzeugung von normalverteilten Zufallszahlen, die essenziell für Monte-Carlo-Simulationen sind. Die Datei Option.cpp definiert allgemeine Parameter und Methoden für die Preisberechnung und Sensitivitätsanalyse, während EuropeanOption.cpp, AsianOption.cpp und AmericanOption.
cpp jeweils spezialisierten Code für die verschiedenen Optionsarten enthalten. Die Trennung der Implementierungen erleichtert die Erweiterung und Wartung des Systems. Die praktische Anwendung des Programms wird durch die main.cpp gesteuert. In ihr werden die grundlegenden Marktparameter wie Spotpreis, Strike, Zinssatz, Volatilität und Laufzeit definiert.
Auf Grundlage dieser Eingaben werden dann die unterschiedlichen Optionsklassen instanziiert, ihre Preise berechnet und die entsprechenden Greeks ausgegeben. Der Code ist so aufgebaut, dass er mit geringfügigen Anpassungen auch zur Simulation verschiedener Marktszenarien oder anderer Parameter benutzt werden kann. Die Kompilierung des gesamten Projekts erfolgt über einen modernen C++-Compiler und kann mit einem einfachen Befehl gestartet werden, der alle notwendigen Quelldateien zusammenführt. Die Nutzung von C++17 ermöglicht dabei moderne Sprachfeatures und eine effiziente Ausführung, was insbesondere bei umfangreichen Simulationen von Vorteil ist. Für Anwender und Entwickler, die sich mit der Bewertung von Finanzderivaten beschäftigen, bietet dieses Projekt eine wertvolle Grundlage, um sowohl grundlegende als auch komplexe Optionen realistisch zu modellieren.