Die Kombinatorik ist ein zentrales Teilgebiet der Mathematik, das sich mit der Untersuchung von endlichen oder abzählbaren diskreten Strukturen beschäftigt. Sie bildet die Grundlage für viele weitere Disziplinen wie die Graphentheorie, Logik, Algorithmik und Statistik. Eine besonders bedeutende Rolle in der Entwicklung der Kombinatorik spielte der niederländische Mathematiker Nicolaas Govert de Bruijn. Seine innovativen Ansätze und umfassenden Lehrmaterialien haben die moderne Kombinatorik entscheidend geprägt und sind bis heute von großer Relevanz. Nicolaas Govert de Bruijn wurde 1918 geboren und gilt als einer der einflussreichsten Mathematiker des 20.
Jahrhunderts im Bereich der diskreten Mathematik. Seine Forschungsarbeit und Schriften umfassen eine Vielzahl von Themen, vom Verhalten spezieller numerischer Reihen über Geometrie bis hin zu ausführlichen Untersuchungen kombinatorischer Strukturen. Ein bemerkenswertes Werk in der Vermittlung kombinatorischen Wissens sind die von J.W. Nienhuys zusammen mit Ling-Ju Hung und Ton Kloks herausgegebenen Übersetzungen der handschriftlichen Vorlesungsnotizen von de Bruijn aus den 1970er und 1980er Jahren an der Technischen Universität Eindhoven.
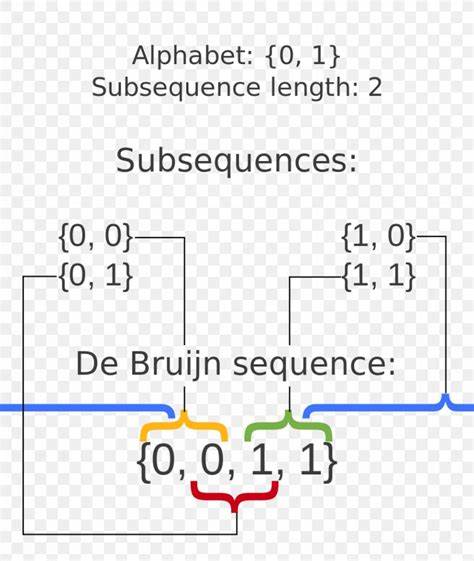
Diese über 190-seitigen Dokumente sind eine wertvolle Quelle für Studenten, Forscher und Interessierte, die einen tiefgehenden Einblick in die Grundlagen und fortgeschrittenen Techniken der Kombinatorik suchen. Die kombinatorischen Methoden von de Bruijn zeichnen sich durch ihre Eleganz und klare Struktur aus. Im Zentrum steht häufig die systematische Analyse von Zählproblemen, bei denen es darum geht, die Anzahl möglicher Konfigurationen unter bestimmten Einschränkungen zu bestimmen. Ein klassisches Beispiel hierfür sind De-Bruijn-Sequenzen, die eine minimalistische Darstellung aller möglichen Kombinationen von Zeichenlängen auf einem gegebenen Alphabet bieten. Diese Sequenzen sind nicht nur ein interessantes mathematisches Phänomen, sondern finden auch Anwendung in der Informationstheorie, Kryptographie und sogar in der Molekularbiologie bei der Analyse von DNA-Strängen.
Neben den De-Bruijn-Sequenzen erforschte de Bruijn umfangreich graphentheoretische Elemente, die eng mit der Kombinatorik verknüpft sind. Er war maßgeblich an der Entwicklung von Theorien beteiligt, die es erlauben, komplizierte Netzstrukturen sowohl zu visualisieren als auch algorithmisch zu analysieren. Solche Theorien sind heute unerlässlich für das Verständnis komplexer Netzwerke etwa in Computernetzwerken, sozialen Medien oder biologischen Systemen. Ein weiterer wichtiger Beitrag von de Bruijn liegt in der konstruktiven Kombinatorik, die sich nicht nur mit der Existenz von bestimmten Objekten befasst, sondern auch effektive Methoden liefert, um diese konkret zu erzeugen. Dies ist insbesondere im Bereich der Algorithmik von Bedeutung, wo schnelle und effiziente Berechnungen combinatorischer Strukturen gefragt sind.
Die Bedeutung der von de Bruijn vermittelten Konzepte erstreckt sich außerdem auf die Analyse von Permutationen und Partitionen. Diese Bereiche untersuchen die verschiedenen Möglichkeiten, Objekte zu ordnen oder in Gruppen zu unterteilen, was eine zentrale Rolle in der Statistik, Optimierung und sogar in der theoretischen Physik spielt. Durch präzise Formulierungen und methodische Herangehensweisen trug de Bruijn dazu bei, diese komplexen Fragestellungen zugänglicher und lösbar zu machen. Darüber hinaus zeigt sich der Einfluss von De Bruijn in der modernen Informatik. Viele Algorithmen zur Datenkompression, Fehlerkorrektur und Zufallszahlengenerierung basieren auf kombinatorischen Prinzipien, die in seinen Werken behandelt werden.
Besonders bei der Entwicklung von effizienten Such- und Sortierverfahren sind seine Konzepte von großer Relevanz. Neben der reinen Theorie zeichnet sich de Bruijn durch eine didaktische Brillanz aus, die sich in seinen Vorlesungen und dessen handschriftlichen Notizen widerspiegelt. Die Übersetzungen, welche dank J.W. Nienhuys und Kollegen der Öffentlichkeit zugänglich gemacht wurden, erlauben es heutigen Forschern und Studierenden, von dem präzisen und tiefgründigen Denken De Bruijns zu profitieren.
Durch die systematische Darstellung, zahlreiche Beispiele und ausführliche Erläuterungen eröffnen die Materialien einen strukturierten Zugang zur Kombinatorik, der sowohl für Anfänger als auch für Fortgeschrittene wertvoll ist. Ein oft unterschätzter Aspekt der De Bruijn’schen Kombinatorik ist ihre Unternehmung, mathematische Herausforderungen nicht isoliert zu betrachten, sondern interdisziplinär zu verknüpfen. Dieser mittlerweile weithin akzeptierte Ansatz war seiner Zeit voraus und förderte damals bereits den Austausch zwischen verschiedensten Fachgebieten. Die praktische Anwendung der Kombinatorik von de Bruijn findet sich auch in der Computergrafik, wo Kombinationsmuster zur Generierung komplexer visueller Strukturen genutzt werden, sowie im Bereich der künstlichen Intelligenz, speziell bei der Lösung von Optimierungsproblemen und der Analyse großer Datenmengen. Zusammenfassend ist De Bruijns Arbeit in der Kombinatorik ein Beweis für die Vielfältigkeit und Bedeutung dieses mathematischen Fachgebiets.