Bayes‘ Regel in der Odds-Form: Ein Leitfaden für verständliche Wahrscheinlichkeitsrechnung

Die Bayes'sche Regel ist ein fundamentales Konzept in der Wahrscheinlichkeitsrechnung und Statistik, das es ermöglicht, Wahrscheinlichkeiten auf der Grundlage neuer Informationen zu aktualisieren. Während die klassische Darstellung der Bayes'schen Regel oft in Wahrscheinlichkeiten erfolgt, bietet die Odds-Form eine alternative und häufig intuitivere Darstellungsweise, die besonders in Bereichen wie der Medizin, der Sozialwissenschaft und dem maschinellen Lernen Anwendung findet. In diesem umfassenden Text wird die Bedeutung der Bayes'schen Regel in der Odds-Form erläutert, ihre mathematischen Grundlagen erklärt und praktische Beispiele gegeben, die den Nutzen dieser Form verdeutlichen. Die Bayes’sche Regel verknüpft die Wahrscheinlichkeit eines Ereignisses unter Berücksichtigung von bereits bekanntem oder neu hinzugekommenem Wissen. Die klassische Formulierung arbeitet mit bedingten Wahrscheinlichkeiten.

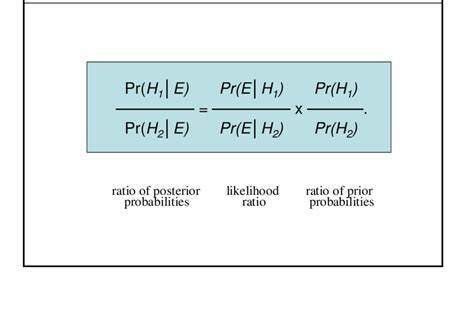
In der Odds-Form hingegen werden Wahrscheinlichkeiten in Quoten (Odds) umgerechnet, was besonders bei der Analyse von Risiken oder diagnostischen Tests hilfreich sein kann. Odds, im Deutschen oftmals mit „Chance“ oder „Quoten“ übersetzt, stellen das Verhältnis der Wahrscheinlichkeit, dass ein Ereignis eintritt, zu der Wahrscheinlichkeit, dass es nicht eintritt, dar. Wenn die Wahrscheinlichkeit für ein Ereignis beispielsweise bei 0,8 liegt, dann sind die Odds 4 zu 1, da 0,8 geteilt durch 0,2 gleich 4 ist. Die Überführung von Wahrscheinlichkeiten in Odds kann komplexe Berechnungen vereinfachen und eine klarere Interpretation von Wahrscheinlichkeitsverhältnissen ermöglichen. Die Bayes'sche Regel in der Odds-Form lautet: Die a-posteriori Odds sind gleich den a-priori Odds multipliziert mit der Likelihood-Ratio.

Die a-priori Odds beziehen sich auf die Anfangschancen vor Betrachtung des neuen Beweises, die Likelihood-Ratio zeigt, wie viel wahrscheinlicher die beobachteten Daten unter der Annahme des Ereignisses sind gegenüber der Annahme des Nicht-Ereignisses. Um dies zu verdeutlichen, betrachten wir ein klassisches Beispiel aus der Medizin: die Diagnose einer Krankheit mittels eines bestimmten Tests. Angenommen, die Prävalenz der Krankheit in der Gesamtpopulation entspricht einer a-priori Wahrscheinlichkeit. Diese wird in a-priori Odds umgerechnet. Dann wird der Testergebnis betrachtet, und die Wahrscheinlichkeit, mit welcher Patienten mit der Krankheit ein positives Testergebnis zeigen, wird der Wahrscheinlichkeit gegenübergestellt, dass gesunde Patienten ebenfalls ein positives Ergebnis zeigen.

Daraus ergibt sich die Likelihood-Ratio, mit der die a-priori Odds aktualisiert und so die a-posteriori Odds bestimmt werden können. Die Umrechnung der Odds zurück in Wahrscheinlichkeiten liefert eine verständliche Einschätzung der tatsächlichen Wahrscheinlichkeit, dass ein Patient mit positivem Ergebnis die Krankheit tatsächlich trägt. Die Vorteile der odds-basierten Darstellung liegen insbesondere in der Klarheit, mit der Veränderungen der Wahrscheinlichkeiten durch neue Informationen dargestellt werden können, sowie in der Einfachheit der Multiplikation im Gegensatz zur komplexeren Division bei Wahrscheinlichkeiten. In der Praxis wird die Bayes'sche Regel in Odds-Form häufig in der Signalverarbeitung und im maschinellen Lernen eingesetzt, etwa bei der Bewertung von Klassifikatoren, die zwischen verschiedenen Zuständen unterscheiden. In der Statistik ermöglicht die Verwendung von Odds eine übersichtlichere Gestaltung von Modellen, was die Zuverlässigkeit von Vorhersagen verbessern kann.

Darüber hinaus wird die Bayes’sche Regel in der Odds-Form in der forensischen Wissenschaft herangezogen, um die Beweiskraft von Indizien quantitativ zu bewerten. Dabei sind die a-priori Odds die Einschätzung der Wahrscheinlichkeit der Schuld oder Unschuld vor Betrachtung der Beweise, die Likelihood-Ratio reflektiert die Aussagekraft des Beweises, und die a-posteriori Odds liefern anschließend die aktualisierte Wahrscheinlichkeit. Trotz der vielen Vorteile ist bei der Anwendung der Bayes’schen Regel in der Odds-Form eine sorgfältige Interpretation essenziell, da falsche Annahmen bei den a-priori Wahrscheinlichkeiten oder bei den Likelihood-Ratios zu irreführenden Ergebnissen führen können. Das Verständnis der mathematischen und konzeptionellen Grundlagen ist deshalb unerlässlich, um korrekte und aussagekräftige Ergebnisse zu erhalten. Die Umrechnung von Wahrscheinlichkeiten in Odds und umgekehrt ist relativ einfach, sollte aber stets genau durchgeführt werden.

Hierzu dient die Formel Odds = p / (1 – p) beziehungsweise die Rückformel p = Odds / (1 + Odds). Diese Rechenwege ermöglichen eine flexible Handhabung der Bayes’schen Regel je nach Anwendungsszenario. Zusammenfassend lässt sich sagen, dass die Bayes'sche Regel in der Odds-Form eine kraftvolle Methode zur Wahrscheinlichkeitsaktualisierung darstellt, die besonders bei komplexen und datenintensiven Aufgabenstellungen klare Vorteile bringt. Ihre Anwendung erstreckt sich von der medizinischen Diagnostik über juristische Beweisführung bis hin zu algorithmischen Entscheidungen in der Wissenschaft und Technik. Wer die Odds-Form beherrscht, kann Wahrscheinlichkeiten präzise interpretieren und fundierte Entscheidungen auf Basis von Daten und Beobachtungen treffen.

Somit stellt die Bayes’sche Regel in der Odds-Form ein unverzichtbares Werkzeug für jeden dar, der in der modernen Statistik und Datenanalyse arbeitet und komplexe Wahrscheinlichkeiten transparent und nachvollziehbar darstellen möchte.