Die richtige Stichprobengröße zu bestimmen, ist eine der zentralen Herausforderungen in der Datenanalyse und Statistik. Egal, ob Sie Marktanalysen durchführen, medizinische Studien auswerten oder Geschäftsentscheidungen auf Basis von Daten treffen – die Genauigkeit und Verlässlichkeit Ihrer Ergebnisse hängen maßgeblich davon ab, wie repräsentativ Ihre Stichprobe für die Gesamtpopulation ist. Ein zu kleine Stichprobe führt zu unsicheren Ergebnissen, während eine zu große Stichprobe unnötige Ressourcen bindet und Kosten verursacht. Doch wie groß sollte eine Stichprobe eigentlich sein? Diese Frage lässt sich nicht pauschal beantworten, denn sie hängt von vielen Faktoren ab und erfordert ein sorgfältiges Abwägen zwischen statistischer Genauigkeit und praktischer Umsetzbarkeit. Zunächst einmal ist es wichtig, den Kontext zu verstehen, in dem Stichproben gezogen werden.
Früher, in Zeiten manueller Datenerhebung, stellten sich Statistiker vor allem die Frage, wie viel Daten gesammelt werden müssen, um verlässliche Erkenntnisse zu gewinnen. Die Datenerfassung war teuer und zeitaufwändig, weshalb der Fokus darauf lag, mit möglichst wenigen, aber dafür sorgfältig ausgewählten Datenpunkten zu arbeiten. Heute hingegen verfügen viele Unternehmen und Forscher über riesige Datensätze, die oft mehrere Millionen Einträge umfassen. Die Herausforderung besteht nun vielmehr darin, eine Aussage darüber zu treffen, wie viel von den gesammelten Daten überhaupt analysiert werden muss, um repräsentative und erschöpfende Ergebnisse zu erhalten. Es geht also darum, einen effizienten und doch aussagekräftigen Teil herauszufiltern.
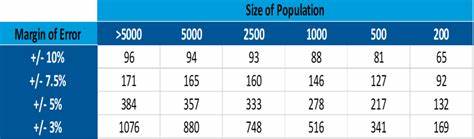
Die wesentlichen Kriterien zur Bestimmung einer angemessenen Stichprobengröße sind die Größe der Grundgesamtheit, der gewünschte Konfidenzgrad sowie die sogenannte Fehlermarge. Die Grundgesamtheit bezeichnet die Gesamtzahl der Objekte oder Personen, über die eine Aussage getroffen werden soll. Dies können beispielsweise alle Kunden eines Onlineshops, sämtliche Patienten in einer Klinik oder alle landwirtschaftlichen Betriebe in einer Region sein. Je größer die Population, desto eher könnte man vermuten, dass auch die Stichprobe größer werden muss. Allerdings stellt sich heraus, dass bei einer ausreichend großen Population die notwendige Stichprobengröße nicht linear mit der Gesamtzahl ansteigt.
Dadurch ist es oft möglich, mit einer relativ kleinen, aber gezielt ausgewählten Stichprobe, auf die Gesamtpopulation zu schließen. Der Konfidenzgrad spiegelt wider, mit welcher statistischen Sicherheit man davon ausgehen kann, dass die Ergebnisse der Stichprobe die Realität der Gesamtpopulation widerspiegeln. Häufig genutzte Werte liegen bei 90, 95 oder 99 Prozent. Ein sehr hoher Konfidenzgrad von 99 Prozent ist beispielsweise medizinisch sinnvoll, da hier Entscheidungen oft lebenswichtige Konsequenzen haben können und Fehler minimiert werden müssen. Bei weniger kritischen Fragestellungen im Business-Kontext kann hingegen ein Konfidenzgrad von 95 oder sogar 90 Prozent ausreichend sein, was die Stichprobengröße deutlich reduziert.
Die Fehlermarge gibt an, wie groß die Abweichung sein darf, mit der die Stichprobenergebnisse von der tatsächlichen Verteilung in der Grundgesamtheit abweichen. In Umfragen oder Studien wird sie gerne in Prozentpunkten formuliert, etwa „±2 %“. Eine niedrige Fehlermarge bedeutet, dass die Ergebnisse genauer sein müssen, was wiederum eine größere Stichprobe erforderlich macht. Steht eine höhere Fehlertoleranz im Raum, reduziert sich die erforderliche Anzahl von Stichprobenpunkten entsprechend. In vielen praktischen Anwendungsfällen beträgt die Fehlermarge zwischen ein und vier Prozent, wobei 2 % ein üblicher Mittelwert ist.
Die Berechnung der notwendigen Stichprobengröße basiert mathematisch auf einer Formel, die diese drei Parameter – Population, Konfidenzgrad und Fehlermarge – kombiniert. Sie sorgt dafür, dass bei der vorgegebenen Sicherheit nicht mehr als die definierte Abweichung auftritt. Um die individuelle Stichprobengröße zu bestimmen, kann man auf verschiedene Hilfsmittel zurückgreifen. Online-Rechner bieten eine schnelle Möglichkeit, erste Abschätzungen vorzunehmen, sollten aber mit Bedacht verwendet werden. Für genauere und an individuelle Bedürfnisse angepasste Analysen empfehlen sich Tools und Bibliotheken in Programmiersprachen wie Python oder R.
Hier lassen sich Berechnungen automatisieren und mit zusätzlichen Faktoren, wie der Varianz der Daten, verfeinern. In der Praxis sind die Daten aber selten homogen. Gerade bei komplexen Populationen mit unterschiedlichen Untergruppen ist es entscheidend, nicht nur die Gesamtzahl zu berücksichtigen, sondern auch sicherzustellen, dass alle relevanten Subgruppen repräsentiert sind. Bei einem Beispiel aus der Landwirtschaft könnten dies unterschiedliche Betriebsgrößen, regional variierende Tierhaltungen oder verschiedene medizinische Behandlungsprotokolle sein. Ein unzureichend geschichteter Stichprobenplan führt dazu, dass bestimmte Gruppen im Ergebnis unterrepräsentiert sind und damit die Aussagekraft der Studie verringert wird.
Die Notwendigkeit der Stichprobensammlung ergibt sich häufig aus praktischen Beschränkungen wie begrenzten Rechenressourcen, Zeit oder Kosten. Trotz moderner Technologien und großer Rechenkapazitäten sind oft nicht alle Daten vollständig oder schnell genug verfügbar. Dies ist beispielsweise bei sehr großen Datenbanken mit Milliarden von Einträgen der Fall. Eine automatisierte und optimal ausgewählte Stichprobe ermöglicht es, trotzdem valide Schlüsse zu ziehen, ohne die Systemperformance oder Projektzeitpläne zu gefährden. Der Strategie, eine gut durchdachte Stichprobe anstelle aller Datenpunkte auszuwerten, kommt somit eine wichtige wirtschaftliche Bedeutung zu.
Neben der statistischen Berechnung ist der sogenannte Test der statistischen Power ein weiterer entscheidender Aspekt bei der Stichprobenauswahl. Die Test-Power beschreibt die Wahrscheinlichkeit, mit der eine echte Wirkung oder ein realer Unterschied auch tatsächlich entdeckt wird. Low-Power-Tests erhöhen das Risiko von Fehlentscheidungen, beispielsweise der Ablehnung einer richtigen Hypothese. Die Power-Analyse wird daher oft eingesetzt, um vor Beginn einer Studie sicherzustellen, dass die eingesetzte Stichprobengröße groß genug ist, um erwartete Effekte statistisch signifikant zu entdecken. Die Auswahl der richtigen Stichprobengröße ist also eine Balance zwischen statistischen Anforderungen und praktischen Rahmenbedingungen.
Eine zu kleine Stichprobe erhöht Unsicherheiten und kann zu Fehlinterpretationen führen. Eine zu große Stichprobe bindet Ressourcen und verlängert Analysezeiten unnötig. Dabei unterscheiden sich die Anforderungen je nach Branche, Forschungsfrage und Datenverfügbarkeit erheblich. Im Marketing können je nach Kampagne schon einige Hundert Befragte ausreichend sein, um Trends zu erkennen. In der medizinischen Forschung mit hohen ethischen und sicherheitsrelevanten Standards sind oft mehrere tausend Probanden erforderlich.
Die Entwicklung von Big Data und datenbankgestützter Analyse hat die Herausforderung der Stichprobengröße besonders in den letzten Jahren stark verändert. Projekte basieren heute oft auf enormen Datenmengen, die an sich wertvolle Informationen enthalten. Doch die echte Kunst besteht darin, die richtige Balance zwischen der Datenmenge und der Analysefähigkeit zu finden, um schnelle, valide und umsetzbare Erkenntnisse zu gewinnen. Moderne Sampling-Methoden ermöglichen es, aussagekräftige Datenpunkte herauszufiltern, ohne die gesamte Datenflut bewältigen zu müssen. Diese Aspekte verdeutlichen, dass es keine universelle Formel für die optimale Stichprobengröße gibt.
Vielmehr ist die Entscheidung immer eine Abwägung, die sorgfältige statistische Planung und fundierte Kenntnisse der konkreten Datenlandschaft erfordert. Wer sich intensiv mit diesem Thema auseinandersetzt, profitiert später von deutlich präziseren Analysen, zuverlässigeren Vorhersagen und wirtschaftlich effizienteren Datenprozessen. Zusammenfassend lässt sich sagen, dass Ihre Stichprobengröße sowohl von statistischen Parametern als auch von praktischen Bedingungen abhängt. Die drei wichtigsten Stellgrößen sind Grundgesamtheit, Konfidenzgrad und Fehlermarge. Für eine verlässliche Stichprobe empfehlen sich Konfidenzniveaus um 95 % und Fehlermargen um 2 %, wobei die erforderliche Stichprobengröße oft im niedrigen tausender Bereich liegt – auch bei großen Populationen.
Die Berücksichtigung der Population und heterogener Subgruppen erhöht die Genauigkeit weiter. Durch moderne Berechnungshilfen, etwa Python-Skripte oder Online-Rechner, kann jeder Datenanalyst schnell und zuverlässig die passende Stichprobengröße für das eigene Projekt ermitteln. Letztendlich stellt ein gut gewähltes Stichprobenvolumen eine entscheidende Grundlage für valide Entscheidungen und erfolgreiche datengetriebene Projekte dar.