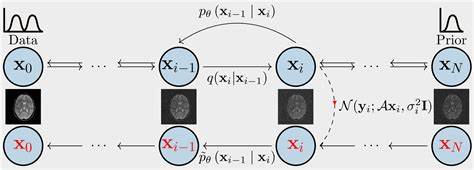
Die Fähigkeit, Daten aus trainierten Machine Learning Modellen rekonstruieren zu können, gewinnt in der modernen Forschung und Anwendung immer mehr an Bedeutung. Gerade in Bereichen wie dem Datenschutz, der modellbasierten Fehleranalyse oder der synthetischen Datenproduktion bietet die Rekonstruktion von Originaldatensätzen einen vielversprechenden Ansatz für neue Erkenntnisse und Anwendungen. Eine der fortschrittlichsten Methoden zur Datenrekonstruktion basiert auf der Bayesschen Inverse Schätzung, die eine robuste und theoretisch fundierte Herangehensweise an das Problem darstellt. Das Kernproblem bei der Datenrekonstruktion aus Machine Learning Modellen kann als sogenanntes inverses Problem formuliert werden: Statt die Vorwärtsfunktion zu nutzen, bei der Eingabedaten zu Modellvorhersagen führen, geht es darum, aufgrund bekannter Modellvorhersagen oder -parameter auf die ursprünglichen Trainingsdaten zu schließen. Dabei steht man jedoch vor einer Vielzahl von Herausforderungen.
Unter anderem ist das inverse Problem typischerweise unterbestimmt und durch Rauschen oder Unsicherheiten gekennzeichnet, was es schwierig macht, eine eindeutige Lösungsmenge zu bestimmen. Hier setzt die Bayessche Inverse Schätzung an, indem sie die Rekonstruktion als ein Problem der Wahrscheinlichkeitsabschätzung betrachtet. Dabei fließen Informationen über vorausgesetzte Wahrscheinlichkeitsverteilungen (Priors), die über die Originaldaten angenommen werden, zusammen mit den Likelihood-Funktionen, die beschreiben, wie wahrscheinlich eine beobachtete Modellvorhersage unter bestimmten Datenparametern ist. Aus dieser Grundlage wird mittels Bayes‘ Regel die posterior-Verteilung geschätzt, die aktualisierte Wahrscheinlichkeitsverteilung der Datenparameter unter Berücksichtigung der Modellinformation. Eine wesentliche Erkenntnis aus der theoretischen Analyse ist die zentrale Bedeutung der Genauigkeit der vorausgesetzten Prior-Verteilungen sowie der Modellgenauigkeit für die Qualität der Datenrekonstruktion.
Liegen die angenommenen Prior-Verteilungen nahe an der tatsächlichen Verteilung der Trainingsdaten, und sind die zugrundeliegenden Machine Learning Modelle sehr präzise, so kann in der Folge eine hochqualitative Rekonstruktion der ursprünglichen Datensätze erfolgen. Das Bayessche Framework bietet ein mathematisch elegantes Werkzeug, um systematisch Unsicherheiten und Abhängigkeiten zu berücksichtigen. Es macht es möglich, nicht nur Punktvorhersagen, sondern vollständige Verteilungen über die rekonstruierten Daten zu modellieren. Durch die Verwendung von Markov Chain Monte Carlo (MCMC) Verfahren, etwa dem Metropolis-Algorithmus, lassen sich so die posterior-Verteilungen numerisch approximieren, auch bei komplexen und hochdimensionalen Datensätzen. Wichtig ist, dass bevor mit der eigentlichen Rekonstruktion begonnen wird, die Trainingsdaten oft durch eine Z-Normalisierung vorverarbeitet werden.
Diese Normierung stellt sicher, dass alle Features auf einer vergleichbaren Skala liegen, was nicht nur die Stabilität der Machine Learning Modelle verbessert, sondern auch die Bayessche Inference auf eine gleichmäßig definierte Parameterdomäne ermöglicht. Die Praxis zeigt, dass selbst mit einer einfachen Annahme wie einem gleichverteilten Uniformprior über einen plausiblen Parameterbereich von etwa −3 bis +3 (entsprechend der Drei-Sigma-Regel bei normalisierten daten), bereits ansehnliche Rekonstruktionsergebnisse erzielt werden können. Allerdings erlauben meist komplexere und datenspezifischere Priors noch bessere Ergebnisse. Solche Priors können beispielsweise hierarchisch aufgebaut sein oder die statistischen Abhängigkeiten in den Daten besser abbilden, was die Rekonstruktionsgenauigkeit weiter steigert. Ein weiterer entscheidender Faktor ist die Modellgenauigkeit.
Modelle mit niedriger Trainingsfehlerquote ermöglichen deutlich bessere Rückschlüsse auf die Trainingsdaten. Anders als bei herkömmlichen Anwendungen, bei denen die Generalisierung auf Testdaten im Fokus steht, ist hier das Trainingsverhalten maßgebend. Denn die Qualität der Rekonstruktion hängt davon ab, wie gut das Modell die Trainingsdaten repräsentiert hat. Modelle mit Unteranpassung (Underfitting) bieten weniger verlässliche Informationen, da sie die Datenmuster unzureichend erfassen. Überanpassung (Overfitting) kann zwar hohe Trainingsgenauigkeit bewirken, bringt aber den Nachteil mit sich, dass das rekonstruierten Datenmodell eventuell Rauschen oder unsinnige Muster reproduziert.
Um diesem Spannungsfeld zwischen Bias und Varianz entgegenzuwirken, kommen verschiedene Optimierungstechniken zur Anwendung. Regularisierungsverfahren wie Dropout oder Gewichtzerfall helfen, die Komplexität des Modells zu kontrollieren und eine bessere Balance zwischen Anpassungsfähigkeit und Generalisierungsfähigkeit zu finden. Datenaugmentation ermöglicht es, die Vielfalt und Menge der Trainingsdaten künstlich zu erhöhen, was wiederum die Robustheit des Modells verbessert. Die methodische Herangehensweise umfasst die Generierung synthetischer Daten, die dem originalen Datensatz möglichst ähnlich sind, basierend auf der geschätzten posterior-Verteilung. Diese synthetischen Daten können verwendet werden, um neue Modelle zu trainieren, sogenannte synthetische Modelle, die oft vergleichbare oder sogar bessere Leistung erbringen als die ursprünglichen Modelle.
Diese Fähigkeit eröffnet vielfältige Anwendungsmöglichkeiten, zum Beispiel bei der sicheren Weitergabe von Daten ohne direkten Zugriff auf originale sensible Informationen. Experimente auf verschiedenen Benchmark-Datensätzen, darunter Herzkrankheitsdaten, Anämietypen und handgeschriebene Ziffern, bestätigen die enge Übereinstimmung zwischen der theoretischen Vorhersage und den empirischen Ergebnissen. Die Kullback-Leibler Divergenz (KLD) wird dabei eingesetzt, um quantitativ die Ähnlichkeit zwischen den geschätzten und den tatsächlichen Verteilungen zu messen. Über verschiedene Szenarien hinweg zeigen sich starke Korrelationen zwischen der Genauigkeit der Prior-Annahmen, der Modellgüte und der Qualität der Rekonstruktion, was die theoretischen Aussagen robust untermauert. Insgesamt liefert die Bayessche Inverse Schätzung ein kraftvolles und fundiertes Instrumentarium, um inverse Probleme in Machine Learning Kontexten anzugehen.
Sie eröffnet neue Perspektiven im Bereich der Modellinterpretation und des Datenschutzes, indem sie es erlaubt, sensible Informationen aus Modellen zurückzugewinnen oder vertrauenswürdige synthetische Datensätze zu erstellen. Das Verständnis der Zusammenhänge zwischen Prior-Wissen, Modellgenauigkeit und Unsicherheiten verbessert nicht nur die Rekonstruktionsergebnisse, sondern bietet auch wichtige Einblicke für die Gestaltung zukünftiger Machine Learning Systeme. Die fortschreitende Entwicklung von Theorien und Algorithmen in diesem Bereich wird entscheidend dazu beitragen, komplexe inverse Probleme zu lösen, und damit eine Brücke zwischen theoretischer Forschung und praktischen Anwendungen schlagen. Im Kontext von Datenschutzbestimmungen, zunehmender Verteilung von Daten über Föderiertes Lernen und Transferlernen sowie dem steigenden Bedürfnis nach erklärbaren Modellen wird die präzise Rekonstruktion von Daten mittels Bayesscher Methodik eine Schlüsselrolle einnehmen. Zusammenfassend lässt sich sagen, dass die Datenrekonstruktion aus Machine Learning Modellen mittels Bayesscher Inversschätzung eine vielversprechende Methode darstellt, die sowohl theoretisch fundiert als auch praktisch anwendbar ist.
Sie verbindet statistische Prinzipien mit moderner Rechenleistung und bietet eine Grundlage für Innovationsschübe in der datengetriebenen Wissenschaft und Technologie.